Nächste Seite: Re: Das neue Auswendig Aufwärts: Graphen, Schaltwerke und Zahlen Vorherige Seite: Re: Das neue Auswendig
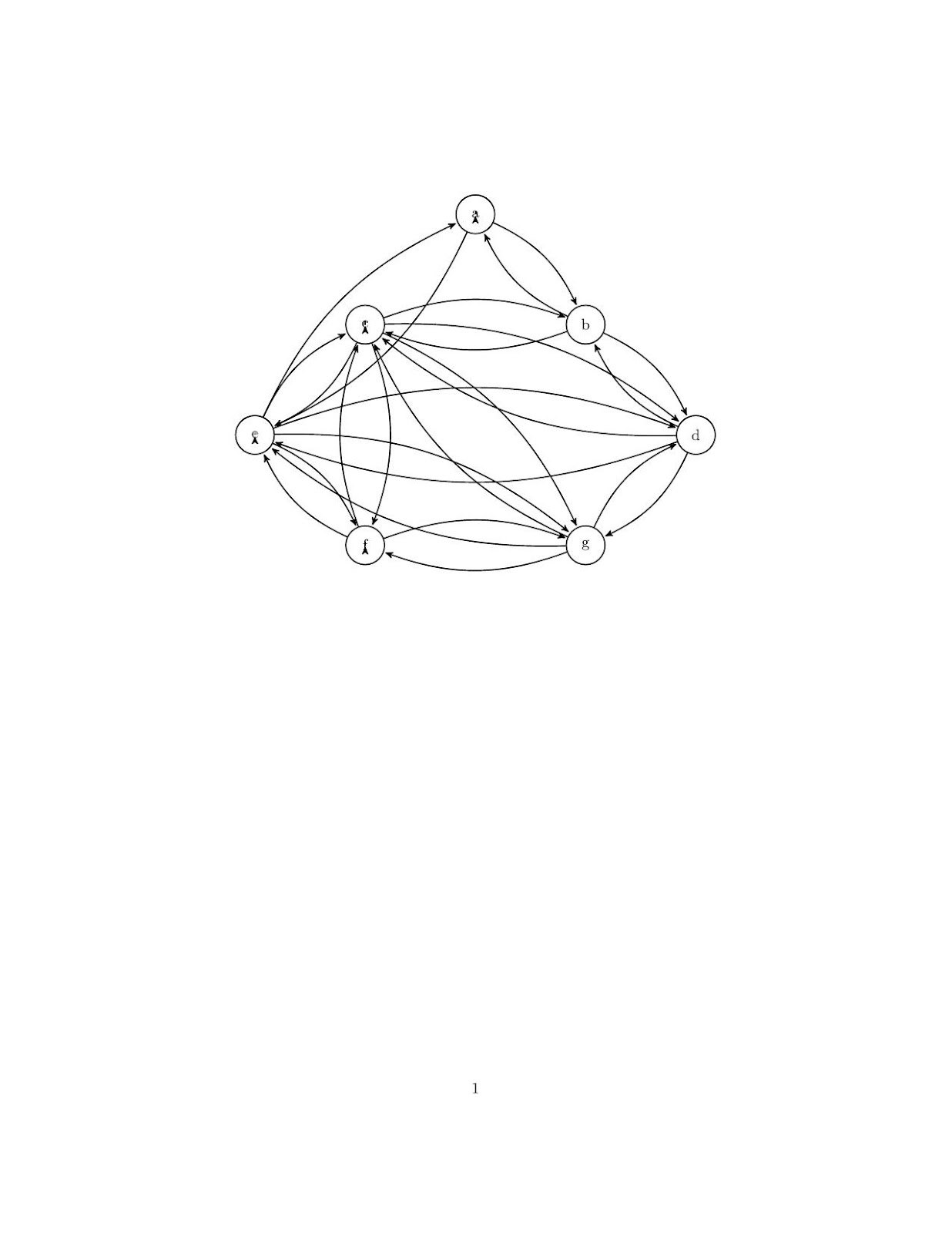
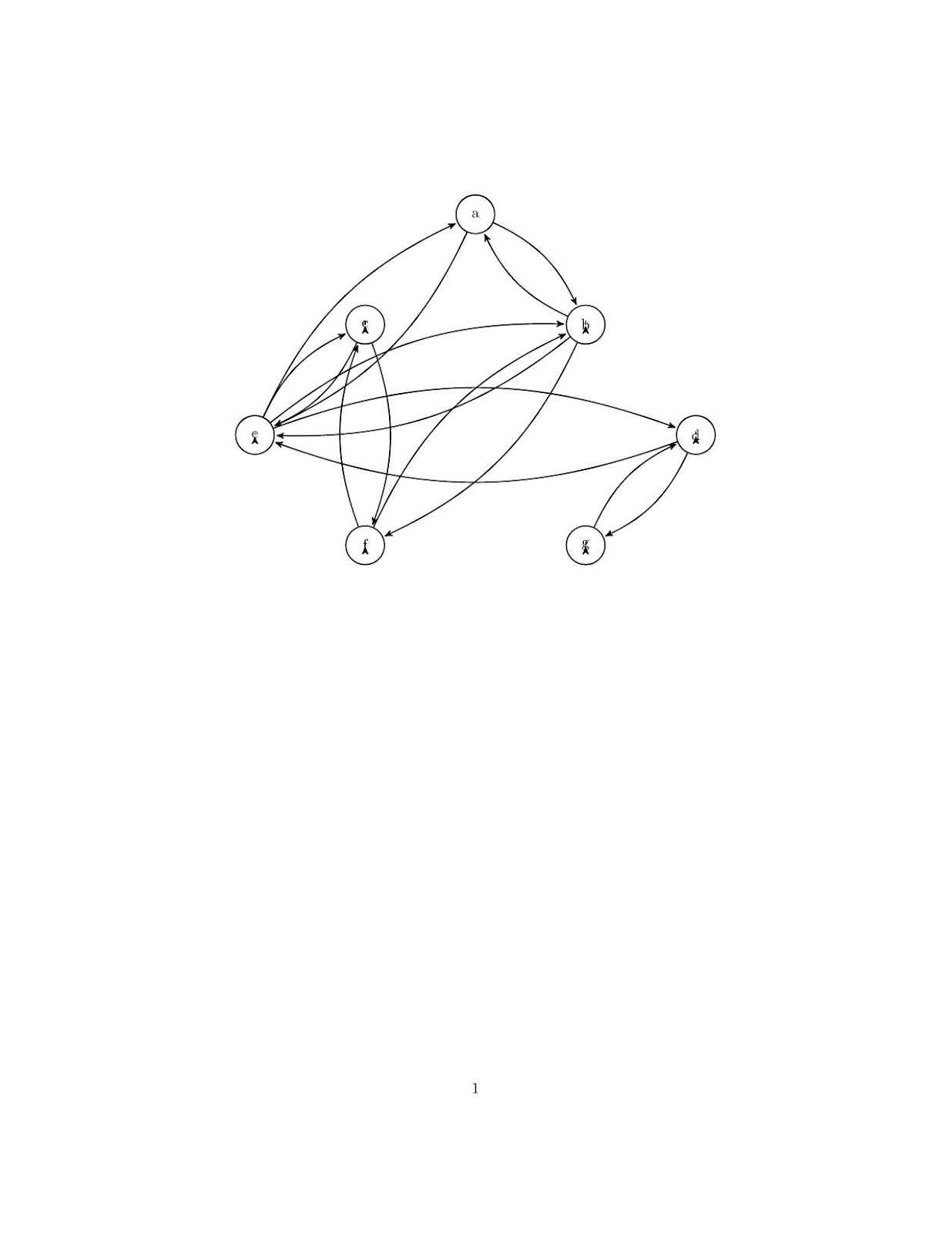
Jetzt mache ich den Algorithmus per hand, aber am Computer
So geht der Algorithmus
pred[r] = r
component[r] = r
Q.Append(r)
while Q.IsNotEmpty():
v = Q.Top()
for w in Neighborhood(v):
if pred[w] == None:
pred[w] = v
component[w] = component[v]
Q.Append(w)
Und jetzt los, ich fange bei zweiten Graphen an, mit Knoten (a)
1.)
pred := {'a', none, none, none, none, none, none}
component := {(a,a)}
queue := {'a'}
2.)
2.1.)
Neighbourhoud ('a') := {'b', 'e'}
component := {(a,a),(b,a)}
pred := {'a','b', none, none, none, none, none}
queue := {'b'}
2.2.)
Neighbourhoud ('a') := {'b', 'e'}
component := {(a,a),(b,a),(e,a)}
pred := {'a','b', none, none, 'e', none, none}
queue := {'e', 'b'}
3.)
3.1.)
Neighbourhoud ('b') := {'a', 'e', 'f'}
component := {(a,a),(b,a),(e,a),(f,a)}
pred := {'a', 'b', none, none, 'e', 'f', none}
queue := {'f', 'e'}
4.)
4.1.)
Neighbourhoud ('e') := {'c', 'b', 'd'}
component := {(a,a),(b,a),(c,a),(e,a),(f,a)}
pred := {'a', 'b', 'c', none, 'e', 'f', none}
queue := {'c', 'f', 'e'}
4.2.)
xx (b)
4.3.)
Neighbourhoud ('e') := {'c', 'b', 'd'}
component := {(a,a),(b,a),(c,a),(d,a),(e,a),(f,a)}
pred := {'a', 'b', 'c', 'd', 'e', 'f', none}
queue := {'d', 'c', 'f', 'e'}
5.)
xx (e)
queue := {'d', 'c', 'f'}
6.)
xx (f)
queue := {'d', 'c'}
7.)
xx (c)
8.)
Neighbourhoud ('d') := {'g'}
component := {(a,a),(b,a),(c,a),(d,a),(e,a),(f,a),(g,a)}
pred := {'a', 'b', 'c', 'd', 'e', 'f', 'g'}
queue := {'g'}
9.)
xx (g)
FERTIG
Die Komponente
C := {(a,b),(a,e),(b,f),(e,c),(e,d),(d,g)}
[/code]
So, ich probiere das jetzt mit einem gewichteten Graphen. Ich suche mir 5 Punkte Mit Google Maps in Tuebingen
Durch Google Maps, lasse ich mir die Abstaende - nicht etwas Koordinaten von jedem Punkt zu jedem Angeben
Ich muss die Abstaende nehmen nicht die Koordinaten (Laenge, Breite), weil zwischen den Punkten sind strassen und ich fliege nicht durch Tuebingen
Die abstaende sind jeweils die Gewichte im Graphen
Ich muss die abstaende per Hand eingeben, sonst muesste ich eine Schnittstelle fuer Google Schreiben
Ich nehme an, das sind
5!
verschiedene Abstaende
Also
5*4*3*2*1
Ich speichere die jeweiligen Abstaende, so wie die Punkte
Ich schreibe den Algorithmus neu und errechne die Summe der Abstaende. Ich suche den laengsten und kuerzesten Weg, mit dem Algorithmus
Nachher laufe ich die Wege durch Tuebingen und lasse mir die vom Smartphone mit google aufgeschriebene Laenge der Route ausrechnen
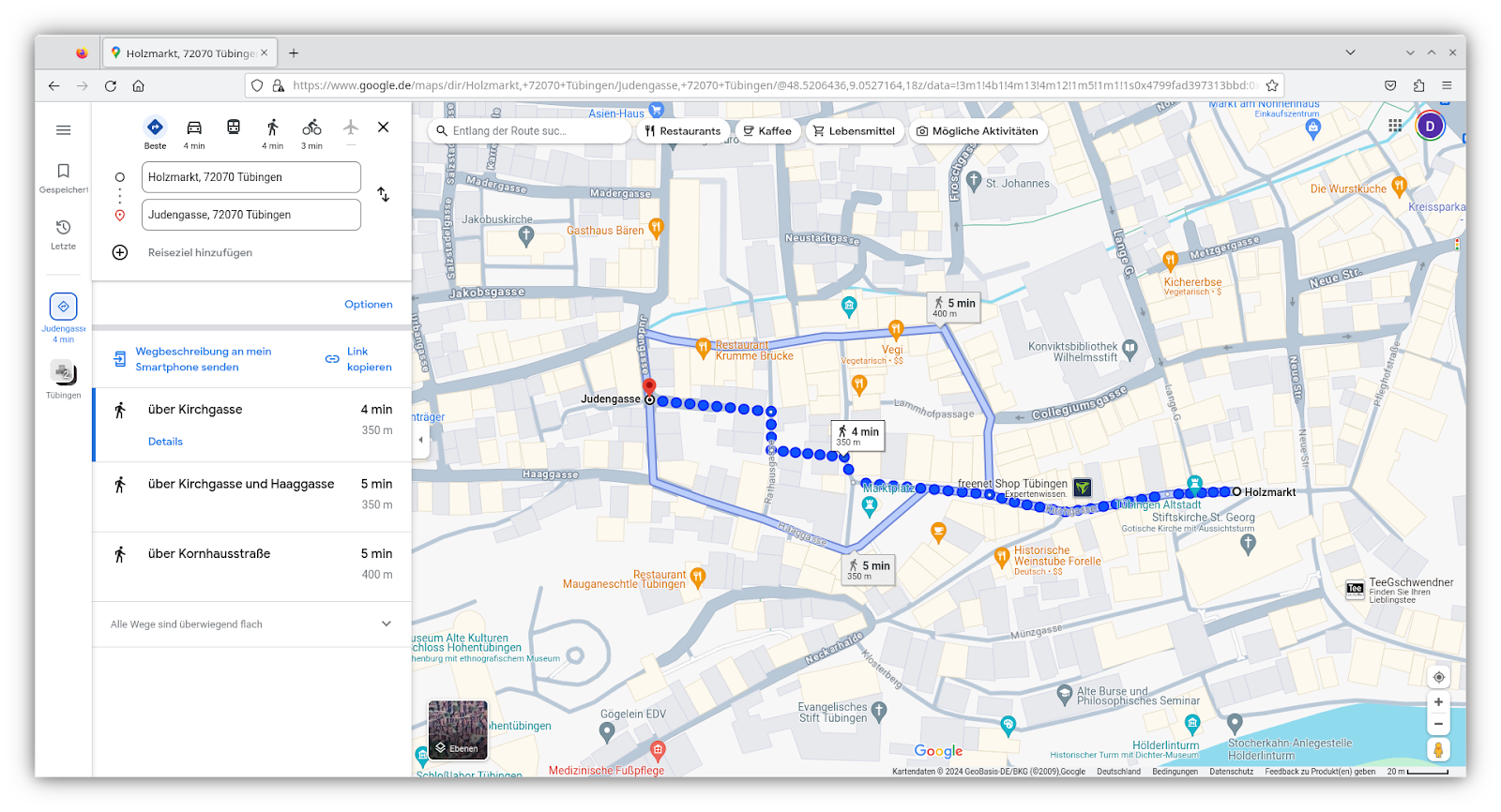
1.) Holzmarkt 2.) Judengasse 3.) Neckarbruecke 4.) Jakobuskirche 5.) Kelternplatz (Holzmarkt, Judengasse) (Holzmarkt, Neckarbruecke) (Holzmarkt, Jakobuskirche) (Holzmarkt, Kelternplatz) (Judengasse, Neckarbruecke) (Judengasse, Jakobuskirche) (Judengasse, Kelternplatz) (Neckarbruecke, Jakobuskirche) (Neckarbruecke, Kelternplatz) (Jakobuskirche, Kelternplatz) (Holzmarkt, Judengasse, 350m) (Holzmarkt, Neckarbruecke, 300m) (Holzmarkt, Jakobuskirche, 500m) (Holzmarkt, Kelternplatz, 600m) (Judengasse, Neckarbruecke, 160m) (Judengasse, Jakobuskirche, 160m) (Judengasse, Kelternplatz, 350m) (Neckarbruecke, Jakobuskirche, 800m) (Neckarbruecke, Kelternplatz, 950m) (Jakobuskirche, Kelternplatz, 220m Es sind nur 4*3*2*1)