Nächste Seite: Re: Endlich tut die Aufwärts: Graphen, Schaltwerke und Zahlen Vorherige Seite: Marx
Ich uebe jetzt zum ersten Mal die eulertour. Zum ersten Mal die eulertour.
Nein, ich sehe schon. Ich habe ja gesagt, heute kommen meine Adidas Sachen. Sie koennen den Beitrag angucken, ich sagte ich mache Marx bis Adidas. Gut, das kommt heute. Zufriedenheit..aber ich sehe ich muss wieder sehr regelmaessig lernen..eulertour ist die selbe Kurseinheit wie tiefen und Breitensuche. Aber das genuegt mathematisch. Ich finde mathematisch ist alles ganz einfach wenn es lernt, aber muss halt sehr drauf achten, das ist Mathematik und erfordert korrektheit
Dafuer uebe ich tiefen und Breitensuche auf dem Papier. Das mache ich weiter. Ich mag meine Mengenschreibweise. Damit habe ich das gut geloest.
Wobei ich feststellen muss, dass es nicht mehr weit ist bis zur Euler Tour. Ich bin jetzt in der tiefen und Breitensuche, das habe ich 100 verstanden. Die uebungen mit der mengenschreibweise ist gut..jetzt nur noch ein Kapitel. Und das ist einfach vom verstehen. Sie sehen ich bin noch nicht ganz auf der hoehe. Der Stress ist erst vorbei wenn Adidas da ist..und Zigaretten muss ich suchen. Aber: Es ist nur ein Kapitel dazwischen. Das ist valenzsequenzen. Ich glaube das versteht man einfach..dann kommt Eulertour..trotzdem finde ich habe ich Recht, mit dem mathematisch korrekt..ich lerne ja nicht so, dass ich am Anfang das Buch kriege, vorne durchlese und hinten loesen will. Manche sagen probieren geht ueber studieren. Ich mache das nicht so..egal ob ich verstehe, ich lerne auswendig. Und ich denke, ich lerne die Eulertour erst auswendig das Thema, bevor ich es anwende
Doch ich fange jetzt an mit eulertour. Vorher die valenzsequenzen. Ich schreibe mir das jetzt alles auf. In meine Stichworte. Wende es aber nicht an. Es ist trotzdem ein alter Traum von mir, mit der Eulertour. Damals am Gymnasium in der 8. Klasse oder so, wollten die Klassenkamerad*innen einen Weg finden, ohne doppelt zu gehen, bei Graphen. Ich probierte es mit dem Zufall. Und dachte wie kann man geschickt sein. Heute weiss ich, es ist eine Frage der Mathematik..bald kann ich das Problem loesen
Ich schreibe meine notizen jetzt auf.
Gut was valenz ist kann man verstehen, die Anzahl der kanten die in einen Knoten rein und raus gehen. Und valenzsequenz kann man auch verstehen..und Handshake lemma auch. Dass sie Summe der Valenzen aller Knoten in einem Graphen immer gerade ist
Jetzt kommt erdoes und gallai (1963)
Ich verstehe den Satz glaube ich. Also, der erste Satz ist, die Gradsequenz ist immer gerade..das ist Handshake lemma. Im zweiten satz: die Summe der Knoten mit ungeraden Knotengrad ist gerade. Das ist logisch, irgendwie. wenn ich den gesamten Graphen nehme ist die Summe gerade. Wenn ich lauter Knoten mit zwei kanten habe und zwei Knoten mit drei kanten..dann sind die mit ungeraden, 2*3. Die Frage ist wenn ich einen dritten habe, mit 3. Das geht ja nicht, weil wohin soll die Kante fuehren Erdoes und gallai..wenn ich irgendeine Folge natuerlicher zahlen habe, als irgendeine 6,8,5,3,dann ist egal, welche Folge natuerlicher zahlen das ist, das die Gradsequenz eines Graphen, ich sage Mal irgendeines Graphen, wenn die Summe gerade ist. Was ist Gradsequenz. Wenn ich 4 Knoten habe, V1,V2,... Dann haben die jeweils den Knoten Grad 2,4,.. Und diese Grade als Folge aufgeschrieben sind die Gradsequenz.
OK, ich habe den Inhalt von erdoes gallai verstanden. Ich lerne meist saetze. Nicht immer alle Beweise..ich denke in dem Falle gehoert das dazu den Beweis zu verstehen..das werde ich mir zur gemuete fuehren. Ach der Beweis ist einfach. Ich sehe, der ist nicht heftig. Ich sehe der Beweis ist einfach. Ich finde in dem Falle gehoert er dazu.
Was eine Eulertour per Definition ist, ist einfach. Das ist einfach Spaziergang im Graphen, also ein Weg, aber wenn jede genau Mal gegangen wird, im Graphen, ist das per Definition eine Eulertour.
So, koenigsberg selber habe ich verstanden..man muss halt auswendig lernen, dass der Fluss pregel heisst, und es gibt vier landgebiete A, B, C, D. Das heisst, zwei Inseln und zwei ufer. Nennt der das..und 7 bruecken Gut. Ich mache gleich weiter, ich muss mir kurz Zigaretten holen
Danke ich lerne jetzt weiter, mal sehen ob ich die Euler Tour heute noch hinkriege.
Hallo, ich habe leider gerade einen wichtigen Termin und Akku gleich leer. Aber ich beginne jetzt schon mit der Eulertour. Ich weiss man soll Sachen nicht im voraus besprechen. aber ich hoffe ich kann heute noch das Haus vom Nikolaus loesen, nicht nur das: Ich hoffe mir gelingt das tuebinger Brueckenproblem. Hier gibt es drei Fluesse, Neckar, Ammer, steinleich, so weit sie nicht unter der Erde verlaufen - wir wissen ja- eine gerade teilt eine Ebene oder unendliche Ebene in genau zwei Haelften. Jetzt stuende der Mathematiker in Tuebingen angeblich vor dem Problem, dass das Wasser unterfuehrt wurde. Ich denke, das ist kuenstlich geschaffen und wir denken uns einen direkten Fluss Problem ist, jetzt sind ja die Bruecken - die Kanten im Graphen, jedes Gebiet, ist so zu sagen, ein Knoten - und die Bruecken stellen die Kanten dazwischen dar. Zwischen den Knoten. Wir sehen wir haben es inzwischen seit Palmer, in Tuebingen mit einem Multigraph zu tun. Das war nicht immer so. Palmer hat mathematisch auf Tuebingen gewirkt. Durch die Fahrraeder gibt es parallele Kanten. Unabhaengig von der Eulertour, kann ich ja jetzt anfangen, den Graphen von Tuebingen schon mal zu zeichnen.
So, ich uebe jetzt die Eulertour.
Mal gucken, ich habe mir ueberlegt, dass ich als erstes - mal in Tuebingen, den Graphen einzeichne. Ach ja, ich muss den Beitrag von vorher fertig machen.
Jetzt habe ich hier halt Tuebingen, mal in google Maps, jetzt muss ich die Bruecken nachschauen Ich muss das ran zoomen - dann ist der Graph schon mal da.
Jetzt machen wir es mal kurz und schmerzlos so - ich kann nicht alles genau sehen, an Bruecken, ich mache die Bruecken = Kanten roter Balken und die Gebiete, Knoten mit blauem Kreis. Es gibt ja mehr Bruecken - im Gegensatz zu Koenigsberg gibt es unglaublich viele, ich kann nicht identifizieren und es geht ja nicht darum, wie bei der Breitensuche, jeden Knoten zu erreichen und eine Komponente her zu stellen - sondern es geht darum jede Kante ein mal gegangen zu sein. Ohne doppelt zu laufen Das sind ja die Eulertouren.
Also, das ist kein Kreis, mit einem Anhang dran
{{a,b},{b,c},{b,d},{d,e},{e,b}}
Also, kein richtiger Kreis.
Gut, dann haben wir das. Und ich muss nachher noch mal weg - leider kommt das Adidas erst morgen, so stand es jetzt doch drin, erst sah es anders aus - aber es kommt erst Morgen und - ich muss nachher noch mal weg - aber ich kuemmere mich um die Eulertour - danach.
OK, mit dem glaube ich es verstanden. Ich hatte es so auch mit wikipedia.de verstanden und mit dem Kurstext.
Ich gehe halt einen Pfad immer weiter - immer weiter - das bedeutet ich gehe einen Kreis und wenn ich das gemacht habe, dann bin ich wieder am Anfang. Und jetzt muss ich einen Knoten aussuchen, wo noch eine freie Kante ist
Die frage ist, welcher ist das?
Das ist halt der Hierholzer Algorithmus.
Ich suche halt einen Kreis, dann den naechsten kreis, dann den naechsten Kreis. Die Frage ist, dabei muss ich einen neuen Knoten fuer den neuen Kreis finden, welcher ist das.
weil ich muss ja wieder anfangen. sonst bin ich eine Kante doppelt gegangen und so vom Prinzip verstehe ich das. In dem Algorithmus in Python im Kurstext verstehe ich paar Funktionen nicht.
Ach nein, das stimmt ja nicht, das ist ja dumm!
Das geht sehr wohl! Gucken sie mal! Ich habe es verstanden
Wenn sie einen anfangsknoten nehmen und sie gehen und das is kreis und an dem Anfangsknoten ist keine weitere Kante zum naechsten Kreis. Dann sind sie den Kreis trotzdem gegangen. Sie haben am anderen Knoten angefangen, als der naechste Kreis
OK - blos, sagen wir Permutation, das ist es nicht. Aber, wenn sie den Kreis gegangen sind, koennen sie ihn ja anderer Stelle anfangen.
Nur da stimmt ja was nicht. Das funktioniert bei zwei Kreisen. Bei drei Kreisen muessen sie ja vom 1. in den 3. Und wenn sie beim 1. beliebig anfangen, koennen sie ja beim 2. nicht beliebig anfangen.
Muss ich drueber nachdenken, ich muss los. das haus vom Nikolaus kann ich jetzt ohne Algorithmus
Das ist gut, was man da lernt, das Postbotenproblem - das haus, kann ich jetzt wie das Pentagramm zeichnen, vom hinschauen - das Pentagramm konnte ich schon ewig, aber das ist keine Mathematik. Und - trotzdem - was mein Problem ist, ich bin nicht so bewandt in Python, hier sieht man die unterschiede, in der Internet Kultur - meine Sprache C - allenfalls, Pascal, Oberon und Bash - Python ist nicht so mein Ding - warum dialekte lernen. Einige verkrampfen sich ihr leben lang darauf. Dafuer ist mein Assembler besser. Aber jetzt habe ich mal pech. Jeder dieser Algorithmen ist entweder in C Sharp oder in Python geschrieben. Das habe ich schon lange beabsichtigt Python gut zu lernen. Aber ist so keine Mathematik. Natuerlich ich das. Pascal ist Mathematik. Computersysteme I/II ist Mathematik. Automaten sind Mathematik Aber das muessen wir nicht ausdehnen - nur ich kann den Algorithmus nicht lesen Ich kann verstehen, suche einen Kreis, suche den naechsten Knoten im Kreis - und suche den naechsten Kreis. Na ja, wenn die letzten ungereihmten geklaert sind, dann mache ich das in C Das ist aber Mathematik. die letzten ungereihmtheiten. Nicht, wie bist du und wie bin ich und so ungefaehr geht das, sondern 100 Ich verstehe den Algorithmus doch
Gucken sich das an. Es genuegt, wenn sie einen Kreis feststellen, in dem Kreis ein knoten und daran den naechsten Kreis machen und wieder so - weil - das ist jetzt nicht mathematisch, das scheint der Hierholze Beweis zu sein
Ich dachte, wenn sie einen Kreis gehen - dann koennen sie ja irgendwo anfangen und wenn sie den falschen knoten haben, nehmen sie den am Anfang. Wenn sie einen zweiten Kreis haben ,geht das. Aber - was ist beim dritten.
Also, sie ein Antidepressivum. Oder Olanzapin. Dann haben sie drei Kreise. Wenn aber der dritte in der Mitte des zweiten ist, dann koennen sie den zweiten nicht fortsetzen, ohne zu wiederholen fuer den dritten
dann geht das doch - weil sie laufen erst den dritten - aber das ja nicht algorithmus
Ich glaube der Hierholze algorithmus tut was anderes - der macht keine Eulertour, sondern stellt fest, dass der Graph eulersch ist
So weit ich sehe, macht, der einen Kreis, dann den naechsten, dann naechsten . Und jetzt wissen sie, dass der eulersch ist. Wenn er das ist, dann koennen sie eine Eulertour machen. Koennen sie das selbstaendig. Angenommen, der Algorithmus tut das.
Dann waere der dritte Kreis - logisch, sie gehen, bevor sie mit dem 2. fertig sind, den driten, und dann auf den zweiten.
Mein Problem ist - was ist, wenn der zweite Kreis, ein weg hat mit 3 Knoten und 2 Kanten und der dritte Kreis, diese ebenso benuetzt
Koennte ja sein, dass er dann nicht eulersch ist, das heisst nicht geloest werden kann, ohne doppelt zu gehen.
Ich habe eine Idee - wir muessen nachgucken, was Kantendisjunk heisst. Ich weiss nur, sie haben eine Vereinigung und eine Schnittmenge. Vereinigung ist eigentlich disjunkt. Dachte ich, ist wohl falsch wenn sie eine disjunkte Menge haben C = A CUP B und dann sind alle Elemente sind nicht B Das heisst es, wohl und das erklaert das Problem - dass jeder Eulersche Graph - Kantendisjunkt ist, ich gucke gleich nach. Das heisst, wenn sie ein Antidepressivum haben und an der einen Seite 2 C und dazwischen eine Verbindung und beide Ringe der 5 Ringer aussen, oder wie viel das ist und innen drin 6 - aber die haben 2 C gemeinsam, dann sind die Kanten nicht disjunkt Dann ist kein Eulergraph, sie koennen ohne wiederholung nicht gehen.
Hier die theorie bestaetigt sich. Disjunkte Mengen, sollte man wissen, sind Mengen, wo die Schnittmenge = Leere Menge ist. Sollte man wissen.
Dann stimmt das. Jetzt gucke ich mir alles noch mal an - ich gucke mir alles an. Vor allem die Lehrsaetze, es gibt drei Bedigungen die AEquivalent sind, was ein Eulergraph ist - disjunkt ist wichtig - Kantendisjunkt nicht Knotendisjunkt. Der Euler Algorithmus von Hierholz scheint nur fest zu stellen, dass es ein Eulergraph ist. Er macht keine Tour - denke ich mir. So, denke ich aktuell. Wenn ein eulergraph ist, dann koennen sie selber die Eulertour machen Der Hierholz geht so - sie machen einen kreis. Suchen irgendeinen Knoten und machen den naechsten Kreis. Wenn nebenbei darin kanten, wegen dem disjunkt, die schon verbraucht wurden, muss man sich halt merken, dann ist kein Eulergraph. Die Eulertour koennen sie selber gehen. Wenn sie wissen, das ist ein Eulergraph, dann gehen sie den ersten Kringel, sobald sie am Knoten sind, der zum zweiten Kringel fuehrt, gehen sie zum zweiten Kringel. Wenn da ein kringel anfaengt, gehen sie den naechsten kringel. das ist rekursiv. Wenn am zweiten Kreis noch ein zweiter Kringel, dann gehen sie den zweiten Kringel. Sie gehen immer die aeusseren Kringel zu erst. Rekursiv. Und - wenn sie dann mit den den Kringeln fertig sind, wieder zurueck im alten, gehen sie den fertig und wenn inzwischen wieder Kringel kommen, ebenso.
Ja, da steht die Bedingung a) G ist eulersch b) G ist zusammenhaengend und alle Knoten haben geraden Knotengrad c) G ist zusammenhaengend und E ist kantendisjunkte Vereinigung von Kreisen Das heisst, ist ja Kantenmenge und die kreise haben kanten, kantendisjunkt.
So, jetzt gucke ich mir die anderen Beispiele an, dann hole ich zigaretten.
Das haus vom Nikolaus laesst sich loesen aber ist kein Eulerproblem - aber ich prophezeihe ihnen, das hauss laesst sich loesen, die Antidepressiva sind unmoeglich zu loesen.
https://programmingwiki.de/images/2/2d/Kerich_VL_bsp_eulerkreis.png">
Das stimmt nicht, was ich gesagt, es ist fasch. Das kann ja nicht sein. Auch das Koenigsberg ist ja - da sieht man es ja. Das ist hier ein richtiges Beispiel. Wenn man dsa Koenigsberg anschaut - dann sind da ja trotzdem gleiche Kanten in einem Kreis. Sind ja trotzdem - was heisst, dann
c) G ist zusammenhaengend und E ist eine Kantendisjunkte Vereinigung von Kreisen.
Stimmte so also nicht. Stimmte nicht.
Also, stimmte so nicht - kann ich mit leben, bin noch am lernen. Ich bin noch nicht so weit. Ich ueberlege noch. Kann ich mit leben, ich denke noch drueber nach. Kann sein, im Kurstext steht was von Kontaktknoten. Kann sein, Olanzapin geht gerade noch. Weil die haben 2 C. Hier steht von Kontaktknoten. Kann sein, nur eine Kante. Aber warum heisst das Kantendisjunkt?
OK, ich vertehe, ich habe das falsch verstanden. Der Eulergraph selber, ist ja quasi ein Weg. Das ist ja ein Weg - der Eulersche Graph. der entspricht zwar dem urspruenglichen Graph, aber er ist ein Weg. anders als der urspruengliche Graph, wo ich beliebig aufschreiben kann so zu sagen, ist das ein geschlossener weg. Das heisst, das ist der urspruengliche graph, nur als Weg und dabei taucht das Wort paarweise diskunkt auf - und das heisst nur eines - in diesem Weg - der so zu sagen, auf dem alten Graph liegt, in dem weg, sind alle Kanten, in dem Weg - paarweise disjunkt Das heisst, die Kanten werden nicht mehrfach gegangen. Das ist die Definition des Eulergraphen. Die Kanten im Graphen sind paarweise disjunkt, das heisst, sie werden nur ein mal gegangen OK, damit ist die Definition perfekt und der Algorithmus muss noch mal ueberlegt werden.
Jetzt doppeldeutig, ganz falsch scheine ich nicht zu liegen, das eine schliesst das andere nicht aus. Halt, das sind zwei Probleme 1.) der Eulergraph ist paarweise disjunkt als weg 2.) Jetzt kommt der Algorithmus. Der kommt von Hierzholz jetzt haben wir 2x paarweise disjunkt. ein mal ist die definition der Eulertour paarweise disjunkt, deswegen war ich abgelenkt, aber der Hierholzalgorithmus, macht sich paarweise disjunkte Kreise im Graph zu nutze Muss kurz drueber nachdenken ,weiss nicht ob es stimmt.
Also, es stimmt vielleicht doch - es gibt 2x kantendisjunkt. Ein mal in der Definition. Ein mal beim Hierholzalgorithmus ch weiss es gerade nicht, ich brauche Zigaretten. ich gehe in den Tabak Laden lasse mir anschreiben
Ich mache jetzt weiter - ich habe mir keinen Tabak Laden aufschreiben lassen. Ich kann mich zwar nicht verhalten - aber ich finde die Mathematik muss nicht auf den Fuessen des Tabakhaendlers geschehen, ich mache jetzt weiter.
Waehle einen beliebigen Knoten v 0 {displaystyle v_{0}} des Graphen und konstruiere von v 0 {displaystyle v_{0}} ausgehend einen Kreis K {displaystyle K} in G {displaystyle G}, der keine Kante in G {displaystyle G} zweimal durchlaeuft.
Wenn K {displaystyle K} ein Eulerkreis ist, brich ab. Andernfalls:
Vernachlaessige nun alle Kanten des Kreises K {displaystyle K}.
Am ersten Knoten von K {displaystyle K}, dessen Grad groesser 0 ist, wird nun ein weiterer Kreis K ? {displaystyle K'} gebildet, der keine Kante in K {displaystyle K} durchlaeuft und keine Kante in G {displaystyle G} zweimal enthaelt.
Fuege in K {displaystyle K} den zweiten Kreis K ? {displaystyle K'} ein, indem der Startknoten von K ? {displaystyle K'} durch alle Knoten von K ? {displaystyle K'} in der richtigen Reihenfolge ersetzt wird.
Nenne jetzt den so erhaltenen Kreis K {displaystyle K} und fahre bei Schritt 2 fort.
Jetzt verstehe ich den Algorithmus noch besser. Ich soll einen Kreis waehlen. Dann durchlaufen. einen knoten mit Grad groesser 0, soll ich den zweiten Kreis machen.d ie fuege zusammen. Jetzt ergibt sich ein neuer Graph, induktiv kann ich an den neuen Graph, einen weiteren hin zu fuegen
Ich weiss nur nicht, mit der Nummerierung. Ich habe ja beim ersten angefangen. Dann war die die nummerierung falsch. da steht ich muss neu nummerieren. Gut - ich weiss, ich probiere das mal aus. mit der Hand. Ich probiere es aus.
Damit habe ich ein Problem
uege in K {displaystyle K} den zweiten Kreis K ? {displaystyle K'} ein, indem der Startknoten von K ? {displaystyle K'} durch alle Knoten von K ? {displaystyle K'} in der richtigen Reihenfolge ersetzt wird.
...
HaHaHa!
Ich habe es endgueltig verstanen
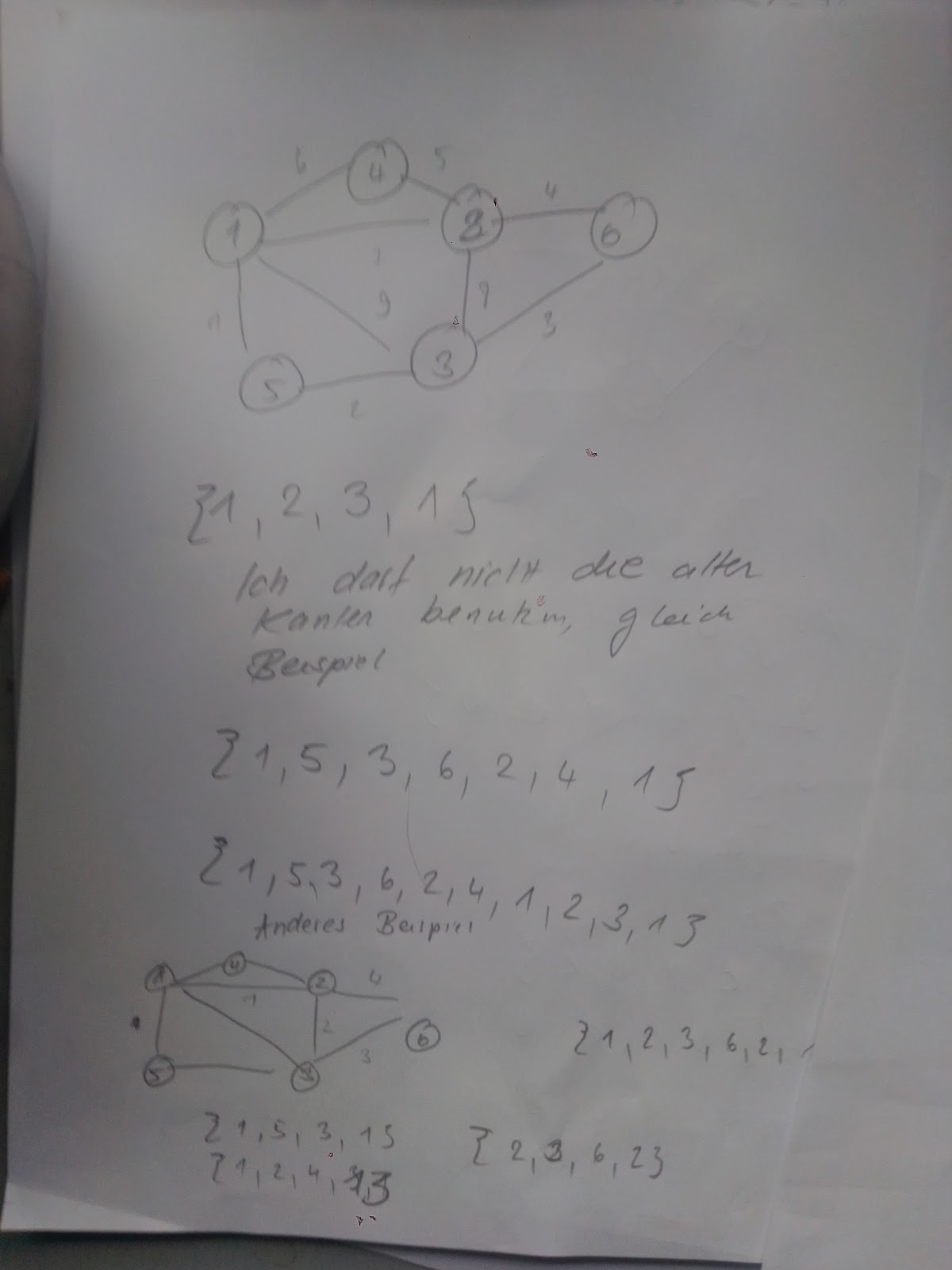
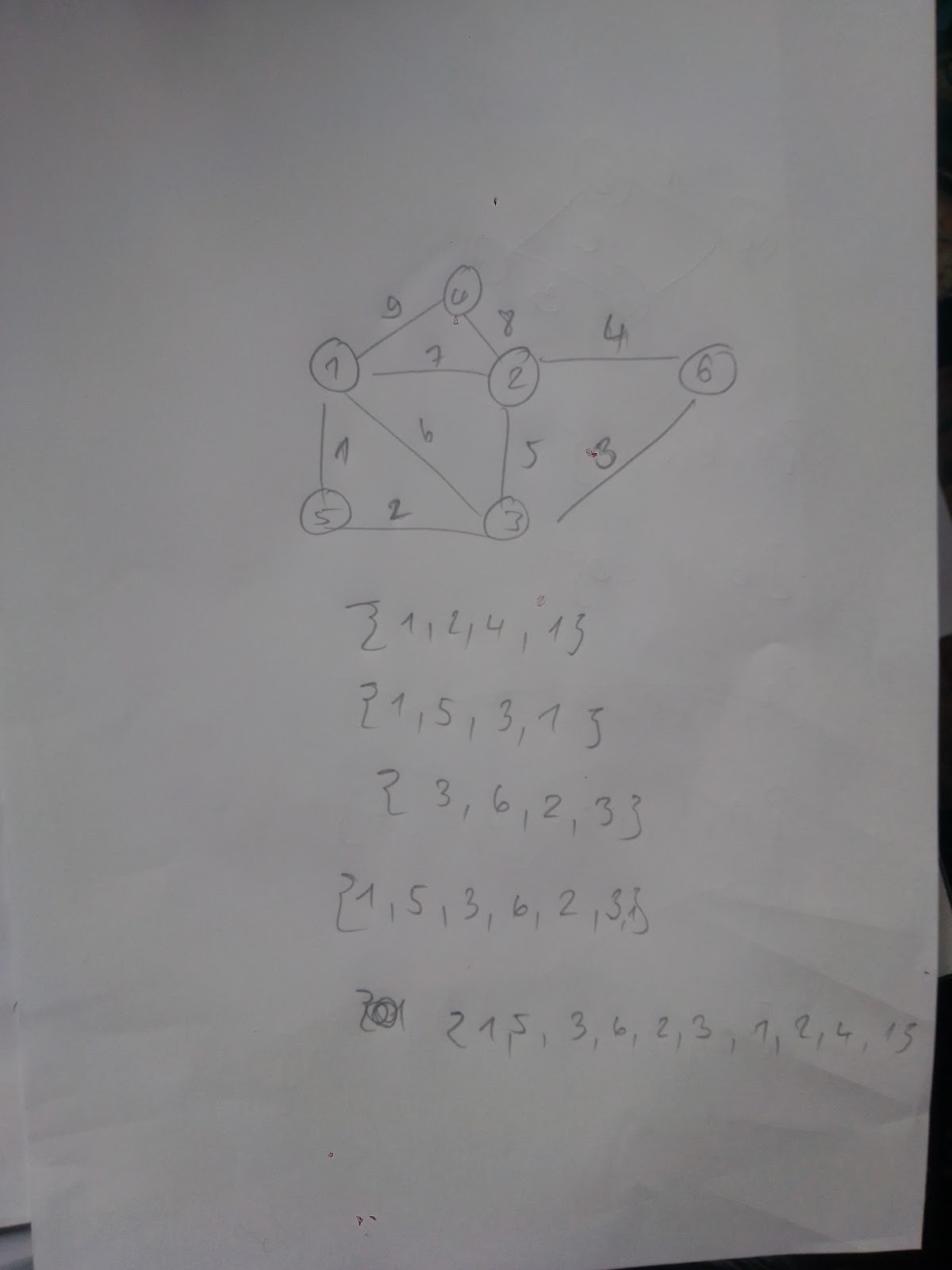
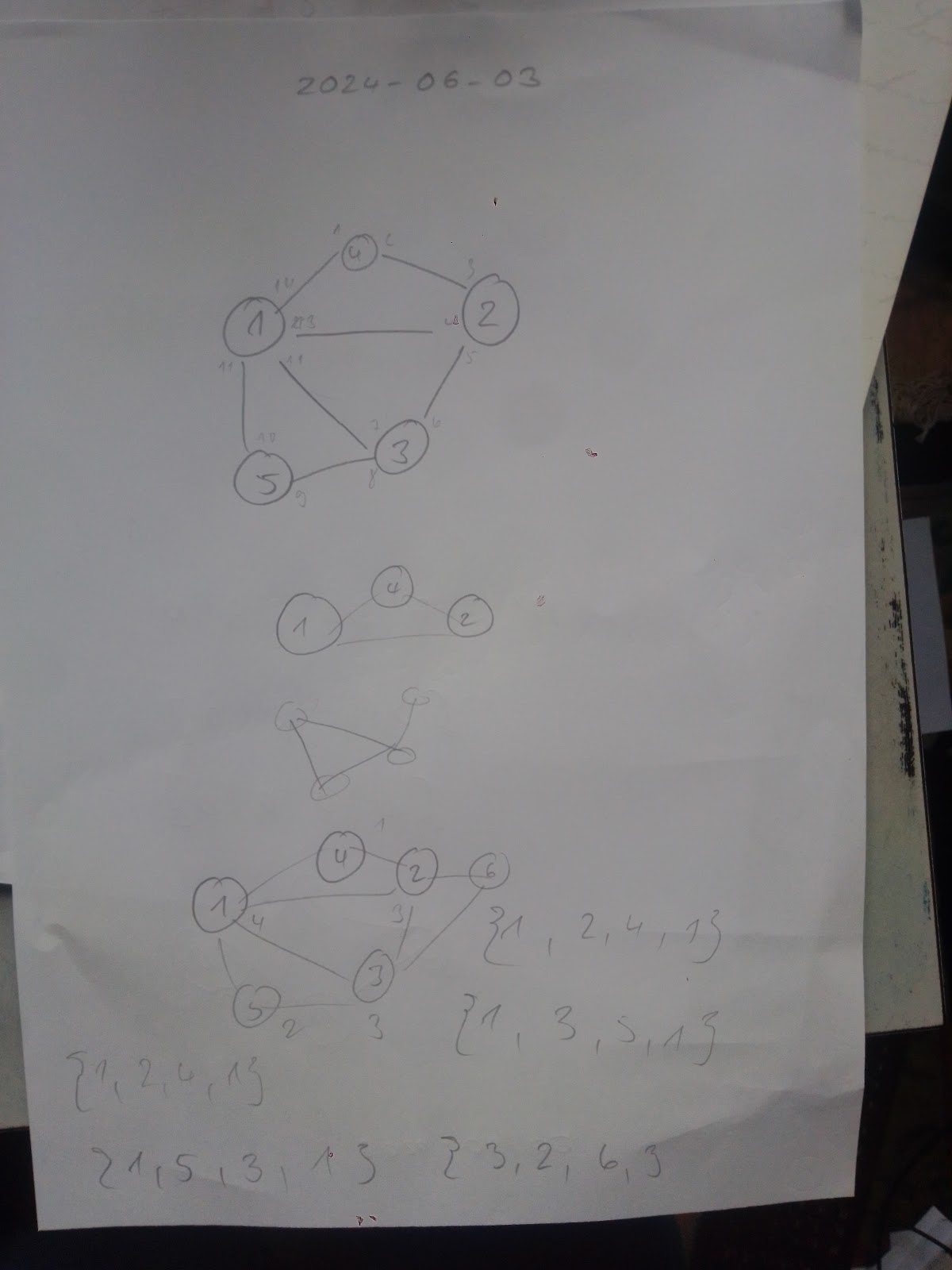
Gegeben sei ein Eulergraph mit neun Knoten (siehe erste Abbildung). Ein Zyklus vom Startknoten 1 waere beispielsweise die in der zweiten Abbildung blau dargestellte Knotenfolge C blau = ( 1 , 2 , 3 , 7 , 1 ) {displaystyle C_{text{blau}}=(1,2,3,7,1)}. Nach Entfernen dieser Kanten haben die Knoten 1, 3 und 7 der bisher gebildeten Zyklus noch einen Knotengrad groesser Null, welche als Startknoten fuer den naechsten Zyklus in Frage kommen. Vom Startknoten 3 aus kann man den Kreis C rot = ( 3 , 1 , 8 , 7 , 4 , 3 ) {displaystyle C_{text{rot}}=(3,1,8,7,4,3)} bilden (siehe dritte Abbildung). Waehlt man nun als Startknoten den Knoten 7, kann man von den uebrig gebliebenen Kanten den Zyklus C gruen = ( 7 , 6 , 9 , 5 , 4 , 9 , 7 ) {displaystyle C_{text{gruen}}=(7,6,9,5,4,9,7)} bilden. Setzt man jetzt C gruen {displaystyle C_{text{gruen}}} in C rot {displaystyle C_{text{rot}}} an Stelle des Knoten 7 ein, erhaelt man den Zyklus ( 3 , 1 , 8 , 7 , 6 , 9 , 5 , 4 , 9 , 7 , 4 , 3 ) {displaystyle (3,1,8,7,6,9,5,4,9,7,4,3)}. Setzt man diesen in C blau {displaystyle C_{text{blau}}} an Stelle des Knoten 3 ein, erhaelt man die moegliche Eulertour ( 1 , 2 , 3 , 1 , 8 , 7 , 6 , 9 , 5 , 4 , 9 , 7 , 4 , 3 , 7 , 1 ) {displaystyle (1,2,3,1,8,7,6,9,5,4,9,7,4,3,7,1)} wie in der letzten Abbildung gezeigt.
Die Abbildung rechts zeigt eine Animation fuer dieses Beispiel.
Ich habe es verstanden, mit dem Beispiel, ich habe es verstanden. Mit dem Beispiel Ich habe einen Kreis 1, 2, 3, 4, 5, 6 So, und jetzt haengen an dem Knoten 2 - ein zweiter Kreis, der geht bis 5 - so zu sagen. der geht 2, 100, 101, 102, 103, 5 Dann mache ich jetzt 1, 2, 100, 101, 102, 103, 5, 6 So ungefaehr. Ich mache den ersten Kreis. Frage wo ist der zweite Kreis - der zweite Kreis ist irgendwo - es haengen viele kreise am ersten Kreis. jeder Knoten, der Grad sagen wir groesser 2 hat - also mehr als zwei Kanten, wird raus genommen und jetzt wird der zweite Kreis gemacht und die alten Kanten nicht wieder verwendet Und jetzt mache ich das rein. Und mit den Kreisen ebenso Ich muss ueberpruefen, ob ich richtig gedacht habe, wenn ja dann gut
OK, habe es verstanden, probiere es auf dem Papier aus.
Ich habe es. Ich zeige ihnen gleich auf dem Papier, dass ich es hinbekommen habe.
Irgendwo ist noch ein Fehler, ich gehe einen Weg doppelt so.
Es kann sein, dass das abgebildete kein Eulergraph ist. Nein, das stimmt nicht, ich wuesste einen Weg, c, b, a, c, d, b Und das ist ein Eulergraph, weil die Summe ist gerade,ich glaube Eulergraph heisst einfach, dass keine Baeume, also nur Kringel dran sind. Das ist Eulergraph. Und die Summe insgesamt der valenz ist gerade und von zwei Knoten bei ungerade muss gerade seun
Nein, das stimmt nicht, ich wuesste einen Weg, c, b, a, c, d, b Und das ist ein Eulergraph, weil die Summe ist gerade,ich glaube Eulergraph heisst einfach, dass keine Baeume, also nur Kringel dran sind. Das ist Eulergraph. Und die Summe insgesamt der valenz ist gerade und von zwei Knoten bei ungerade muss gerade seun
Ich glaube ich weiss wo das Problem ist, ich muss mit einem Knoten anfangen, der eine valenz grosser 2 hat.
Ich probiere Mal einen grossen Graphen.
Ach, so, ich sehe schon da stimmt was nicht. Ich habe ein Problem was ein Eulergraph ist..ich darf die Kante nicht wieder verwenden..wenn die verwendet wurde, darf ich sie nicht noch Mal benutzen. Da liegt ein fehler. ich sage nichts, ich probiere es aus
Ich darf die Kante glaube ich nicht zwei Mal benutzen. Ich muss kurz Pause machen..aber wir sind der Sache auf der Spur.
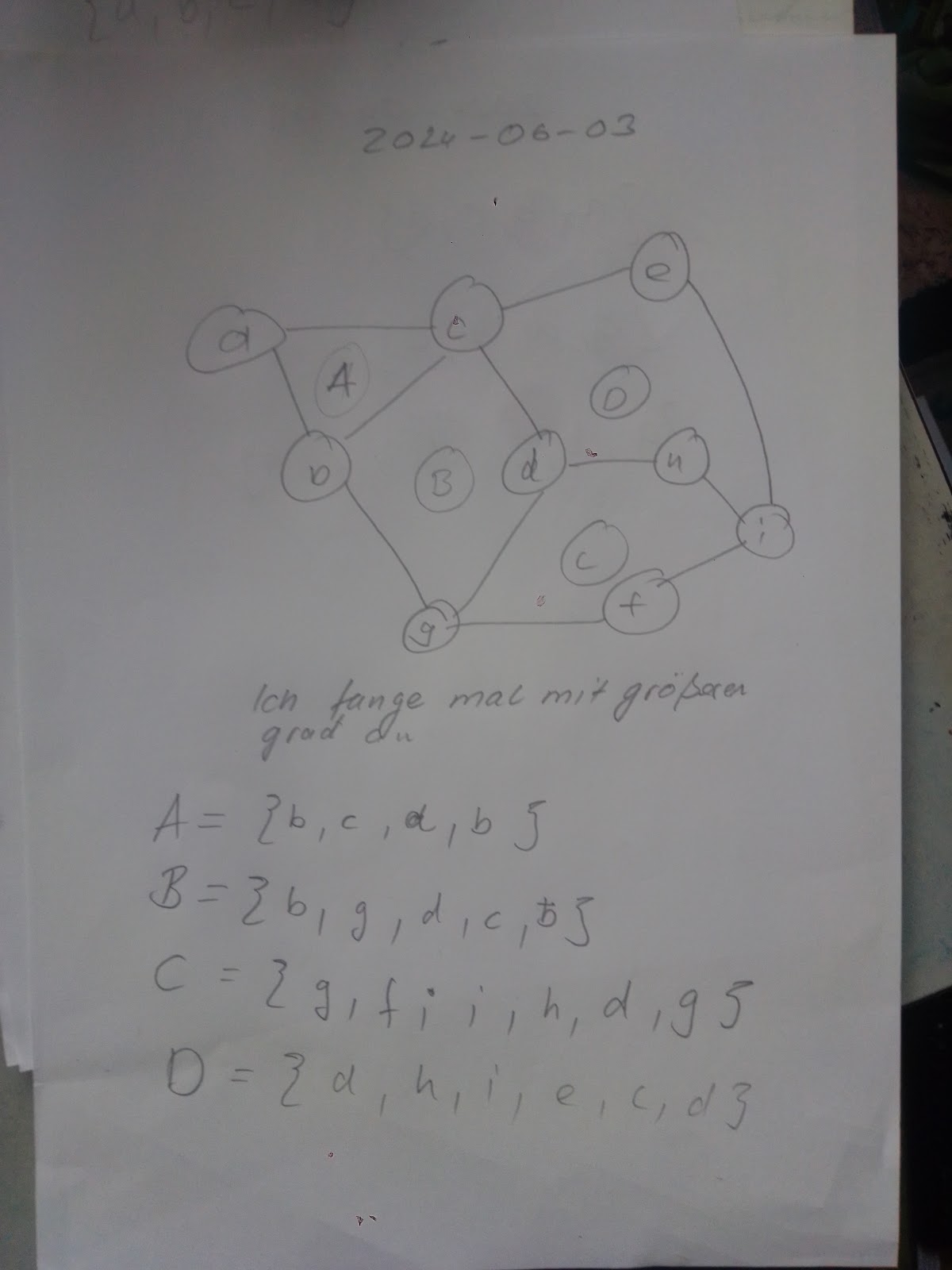
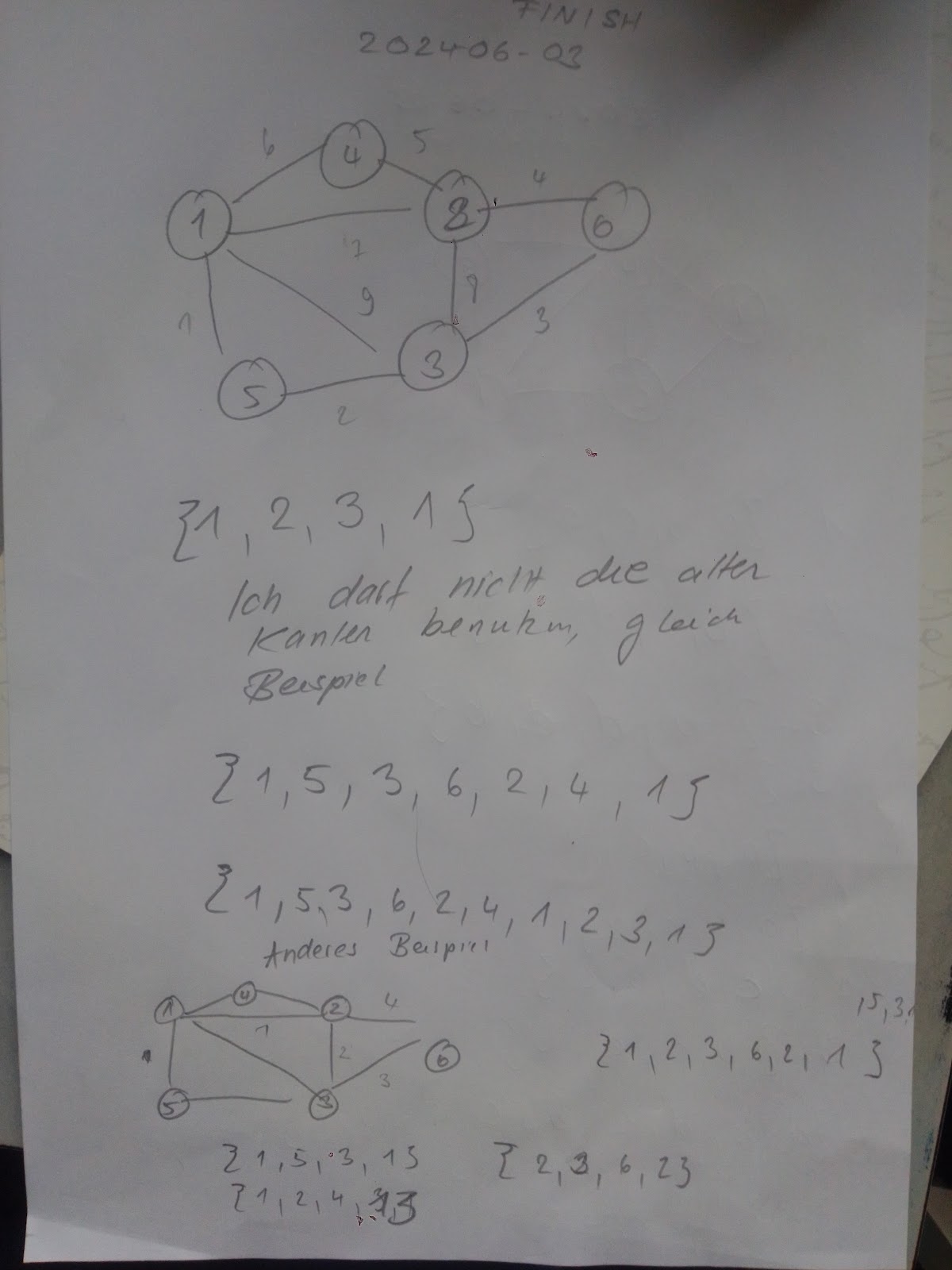
Ich verstehe es! Der Knotengrad ist wichtig. Es geht nur mit Knoten mit geraden Grad. Ich habe es ausprobiert. Ich drei Kreise mit drei Knoten jeweils zusammen gehaengt. Und dabei haben mehrere Knoten den Grad 3. Bei vier kreisen mit drei Knoten. Sind alle Grade gerade, jetzt geht es! Ich zeige Photo!
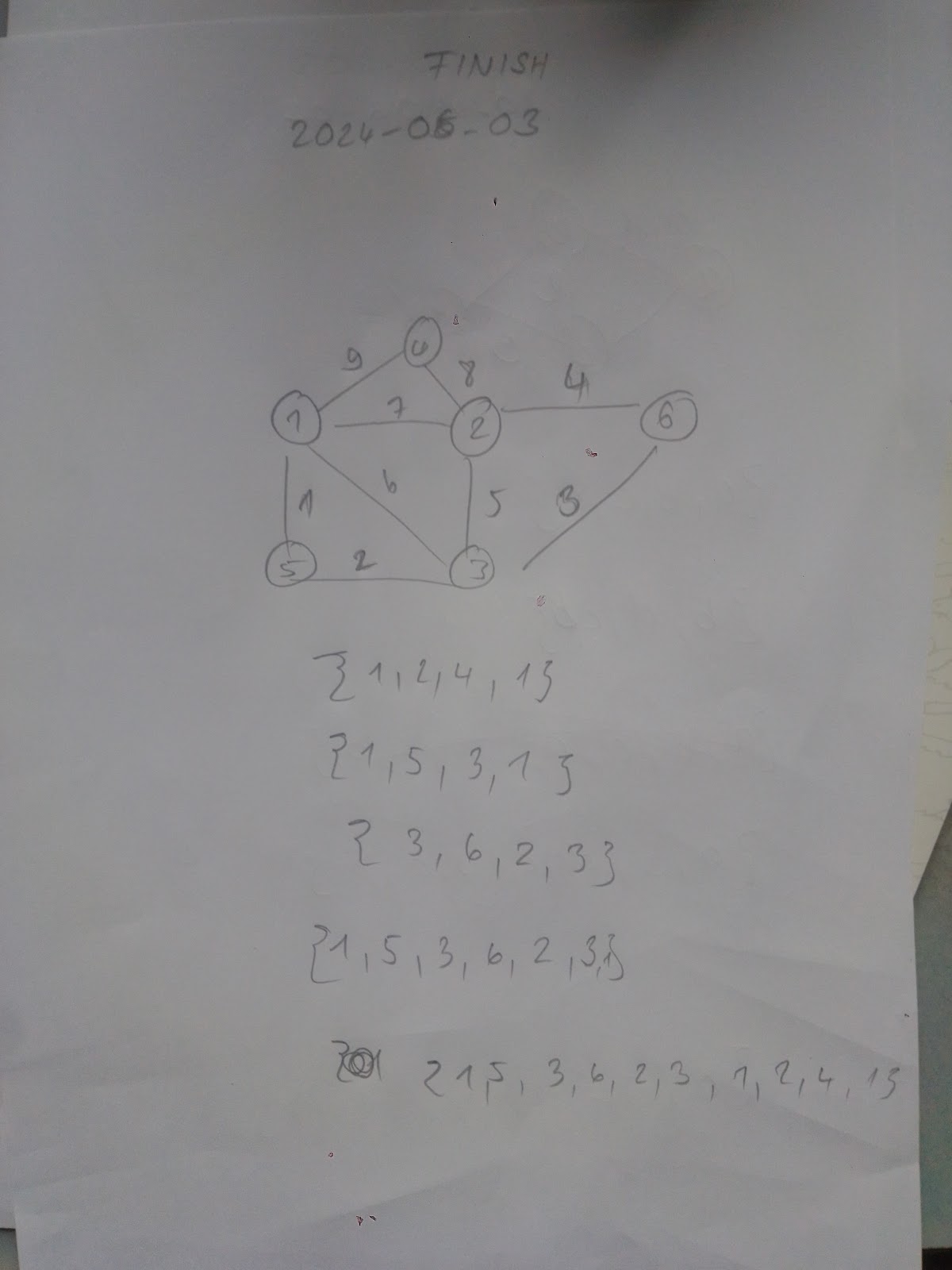
Es hat funktioniert. Zwei Sachen sind wichtig. Die Grade der Knoten muessen gerade sein. Ich darf die Kanten der alte kreise nicht neu verwenden In diesem beiden Beispielen habe ich zwei verschiedene Touren gesucht. Im ersten bin ich gerade los marschiert. Ich habe einen kleinen Kreis gefunden, und dann einen grossen. Im zweiten habe ich mich an das gehalten, ich dachte. Ich habe quasi drei kleine kreise genommen.
Gut, damit ist es passiert, die Eulertour ist sicher. Ich mache noch Datum drauf noch Mal, das ganze kommt auf die Homepage und die naechsten uebungen sind immer mit eulertour.






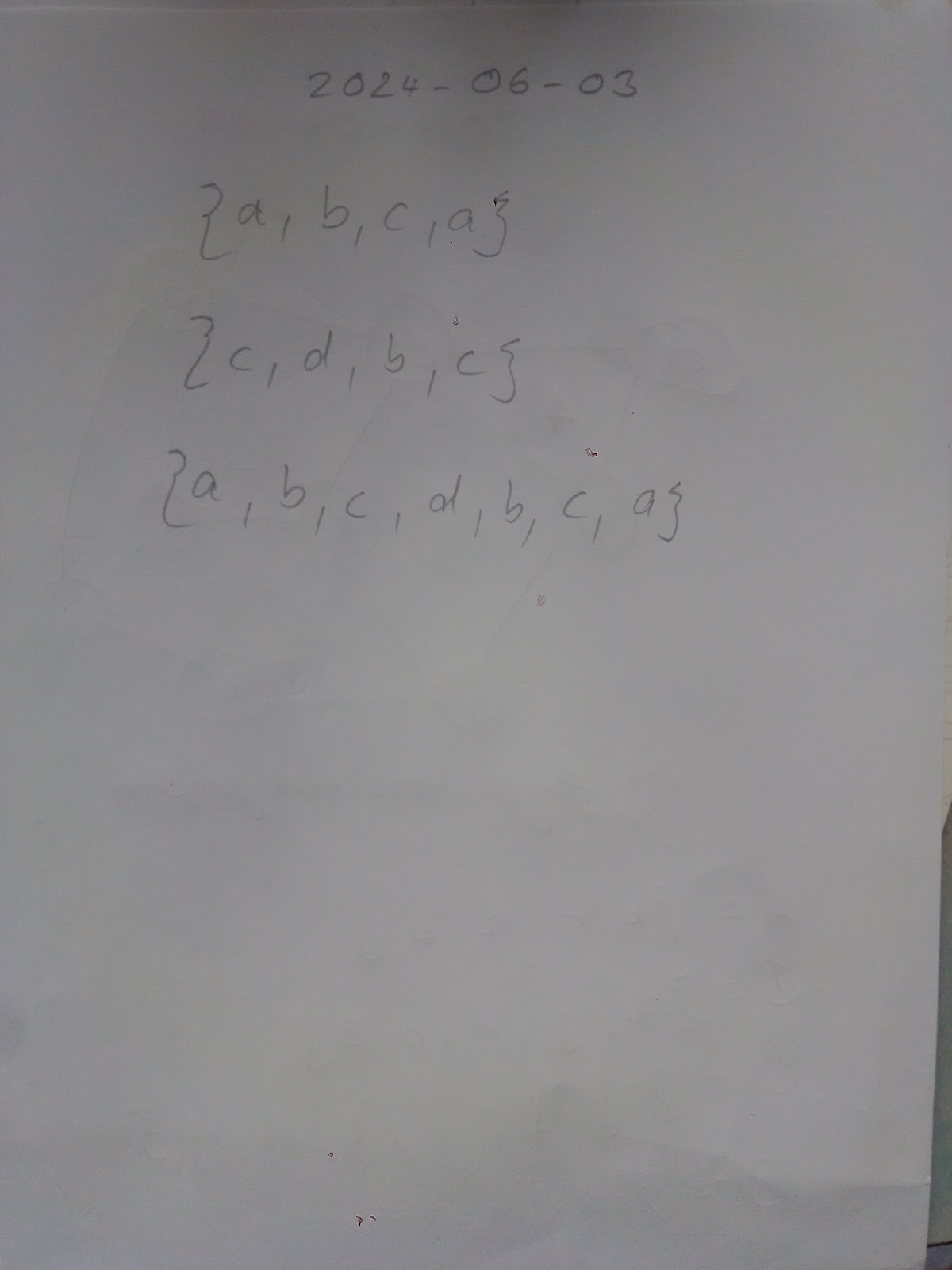

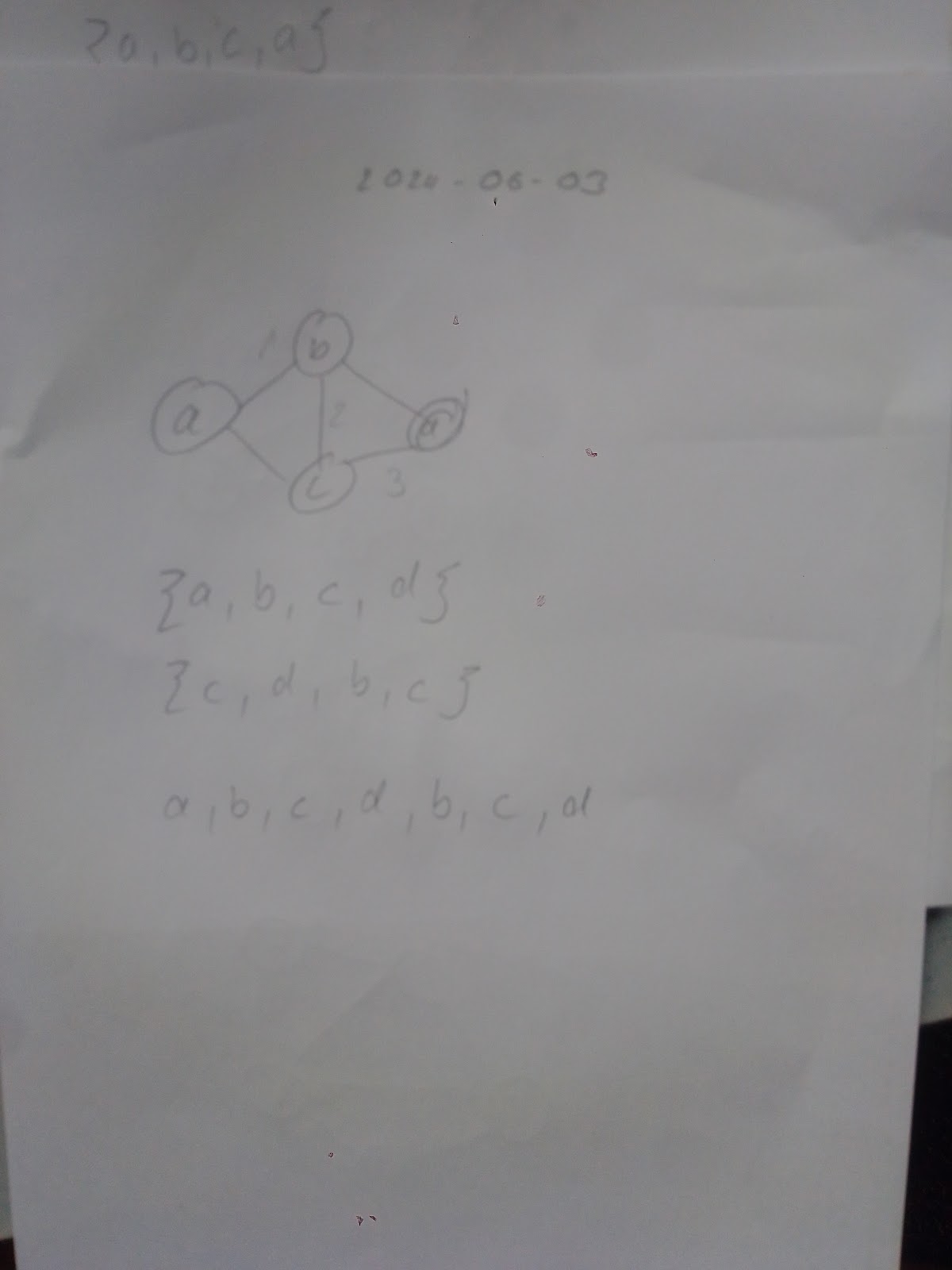


Das Pentagramm ist wohl eine Eulertour, weil jeder Knoten den Grad 2 hat. Also, mit dem Algorithmus wohl loesbar..bloss kommt ein einziger Kreis raus?
Absurdistan. Das Pentagramm ist ein Kreis.
Nein, nicht ganz, nur als Permutation. Fuer Knoten gilt ja: i+(n/2)
Wie auch immer stimmt trotzdem, ein Kreis im Graphen ist v0,e1,V1,e2. Und am Ende zu. Ein Kreis ist i,i+1 und n,0 waehrend ein Weg ohne die Verbindung vom letzen zum ersten ist
Wenn ich die Komponente drauf lege habe ich einen Kreis, zumindest bei einer Permutation
Ach, ja, das heisst, isomorph.
Stimmt das ist ein isomorphismus, das Pentagramm ist isomorph zum Kreis
Das ist sicher so.
Weil im Kreis gehen im Knoten eine rein und eine raus
Das Haus vom Nikolaus hat Knoten mit ungeraden Grad. Es ist ein offener eulerzug, weil start und endknoten nicht uebereinstimmen. Insofern ein anderes problem
Ein offener Eulerzug (auch Eulerpfad oder Eulerweg) ist gegeben, wenn Start- und Endknoten nicht gleich sein muessen, wenn also statt eines Zyklus lediglich eine Kantenfolge verlangt wird, welche jede Kante des Graphen genau einmal enthaelt. Ein bekanntes Beispiel ist das Haus vom Nikolaus.
jeder Knoten in G hat geraden