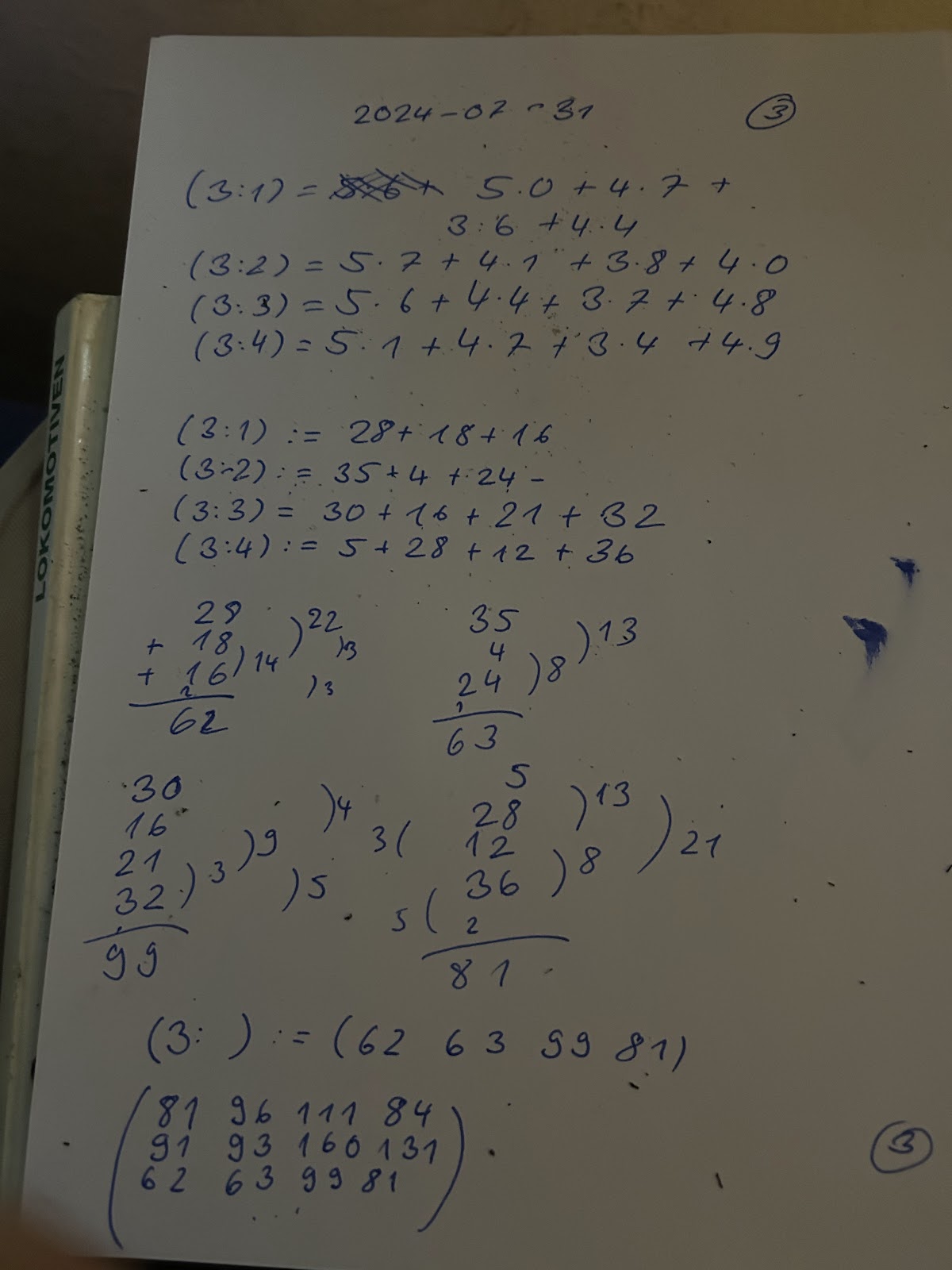Nächste Seite: Re: Das neue Auswendig Aufwärts: Graphen, Schaltwerke und Zahlen Vorherige Seite: Re: Das neue Auswendig
1.) Rechne die Zahl in binaer Darstellung in eine Dezimale Darstellung um
1111010011110000b 62704d
2.) Rechne die Zahl in dezimal darstellung in eine Binaerdarstellung um
24316 0101111011111100
3.) Addiere die drei Zahlen schriftlich
49001
+ 15543
+ 15495
-----------------
80039
4.) Subtrahiere die letzten drei Zahlen schriftlich von der ersten schriftlich
51400
- 6628
- 14100
- 12016
-----------------
18656
5.) Rechne die Zahl ins zweier komplement um, mit 8 Bit - und subtrahiere diese zahl von der ersten und rechne das Ergebnis nach dezimal
-45 -37 = -82
11010011 11011011 = 10101110
6.) Multipliziere die zwei Zahlen schriftlich
56600*15241 = 862640600
7.) Dividiere die zwei Zahlen schriftlich
60020/55485 = 1
8.) Errechne x Logarithmisch mit dem Taschenrechner
14054\^x = 2047129247
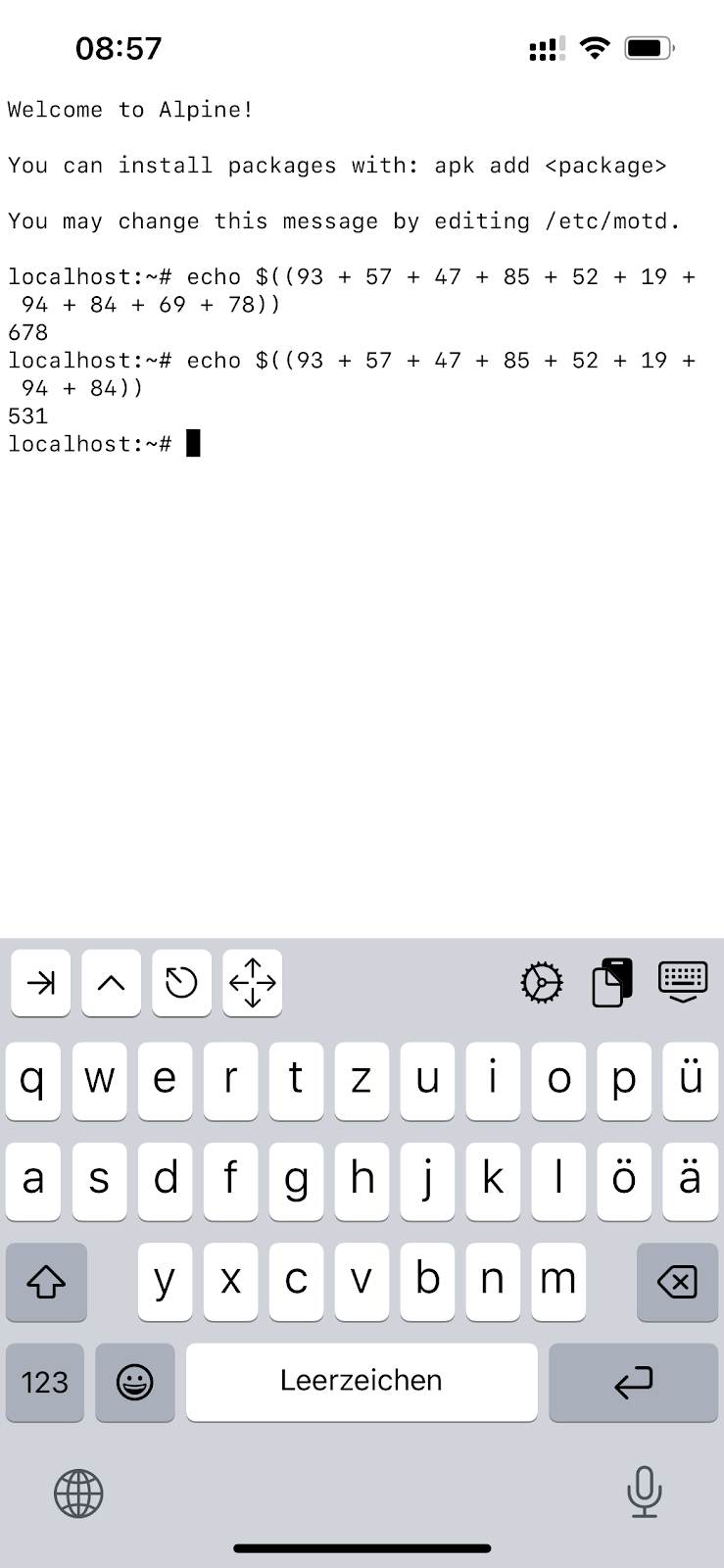
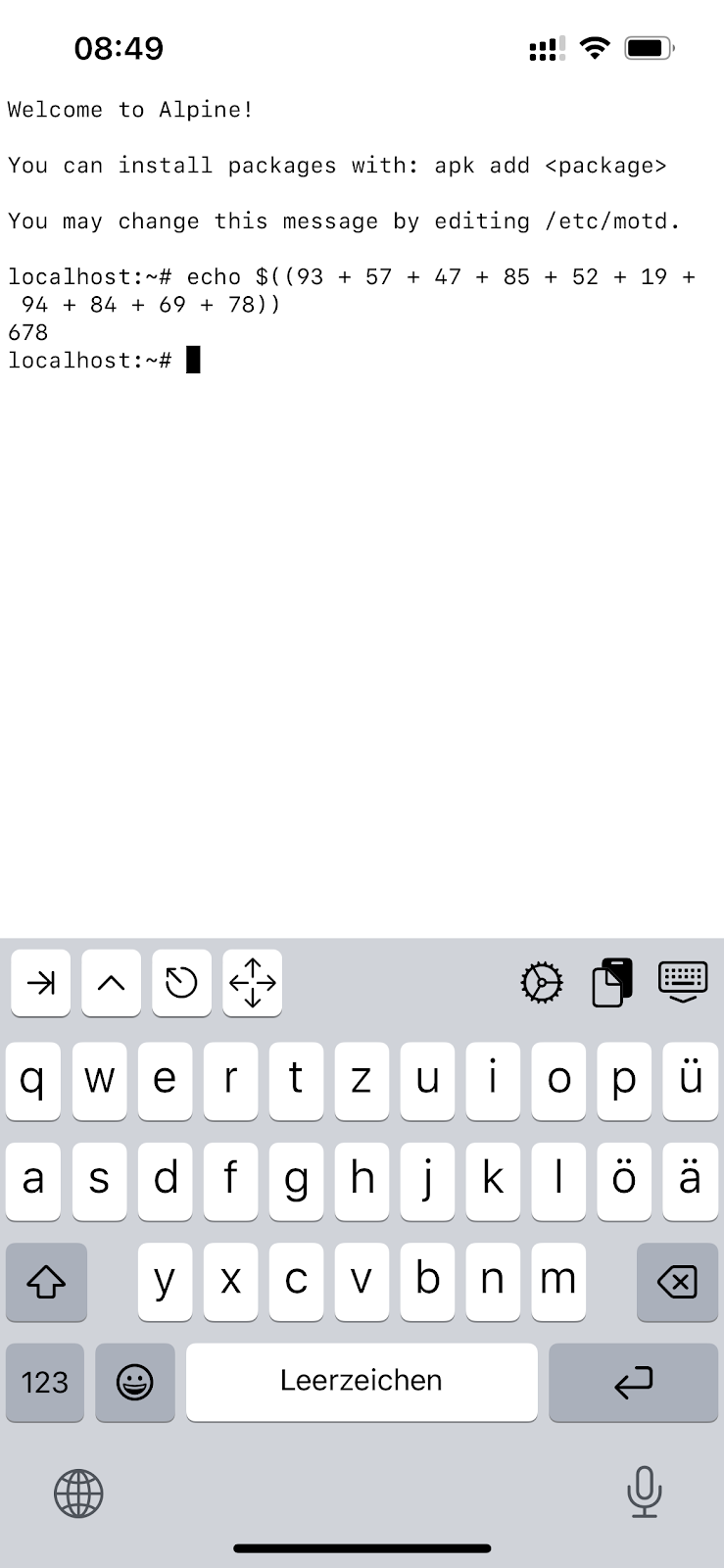
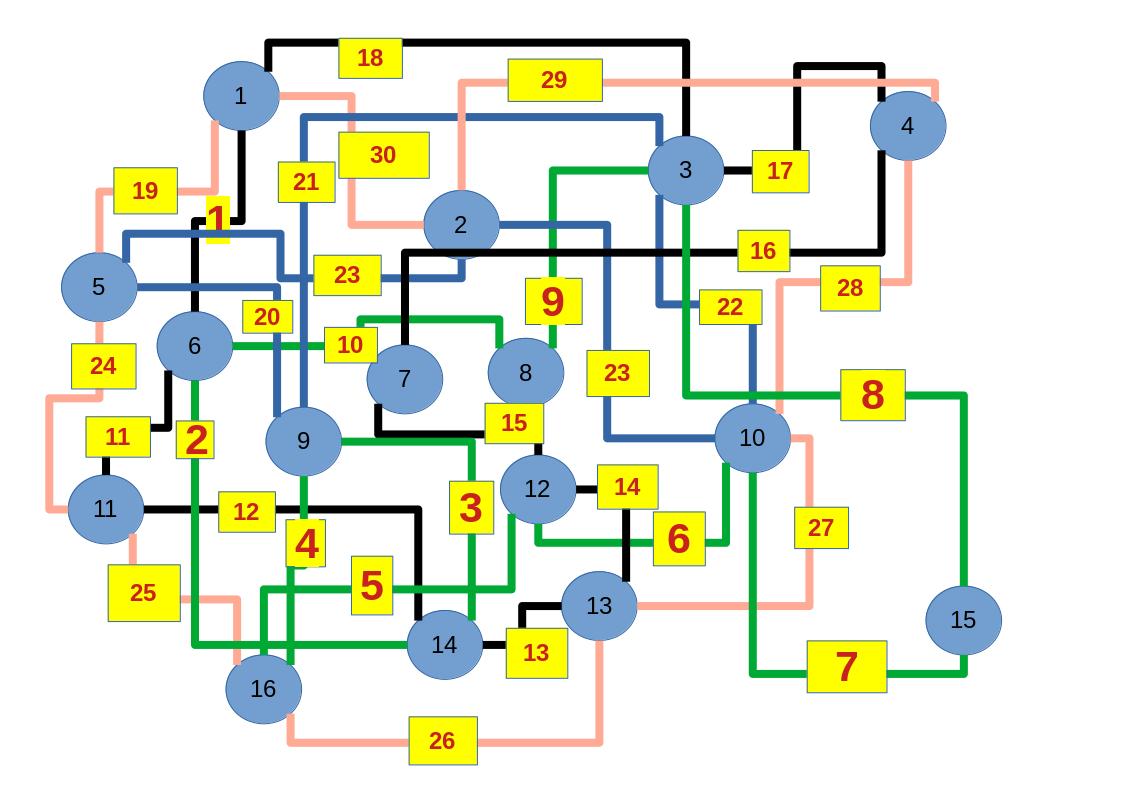
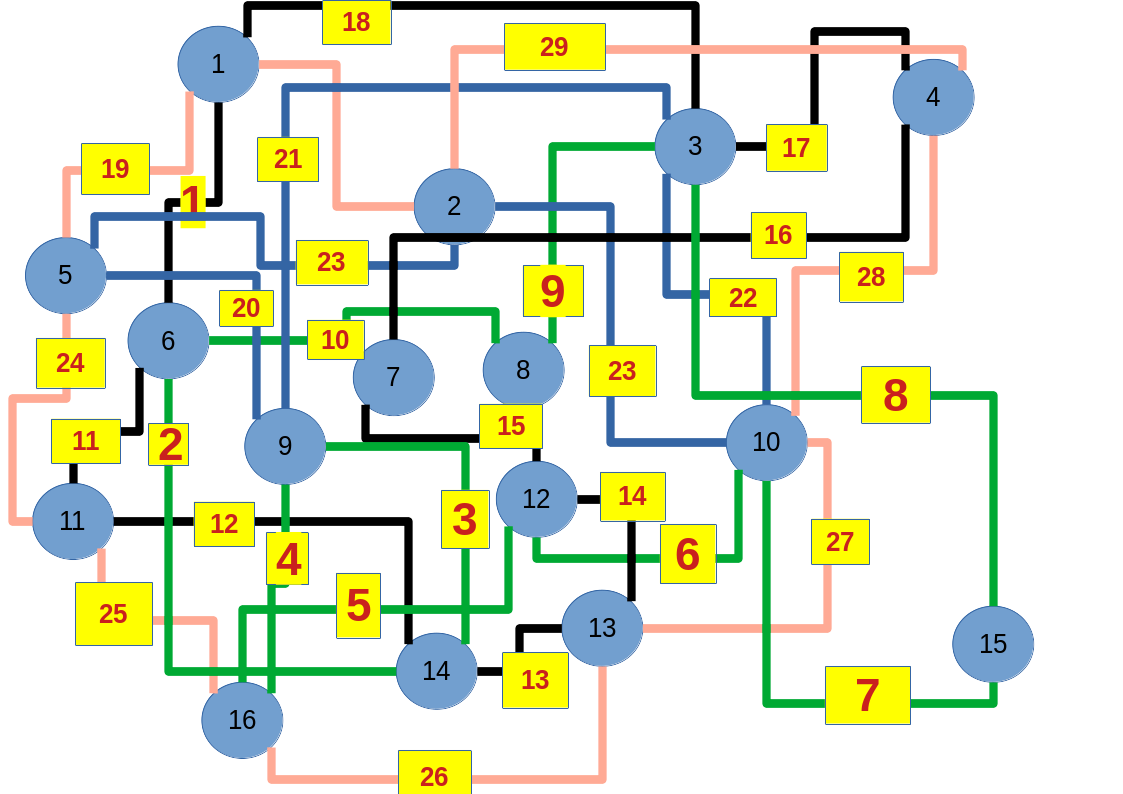
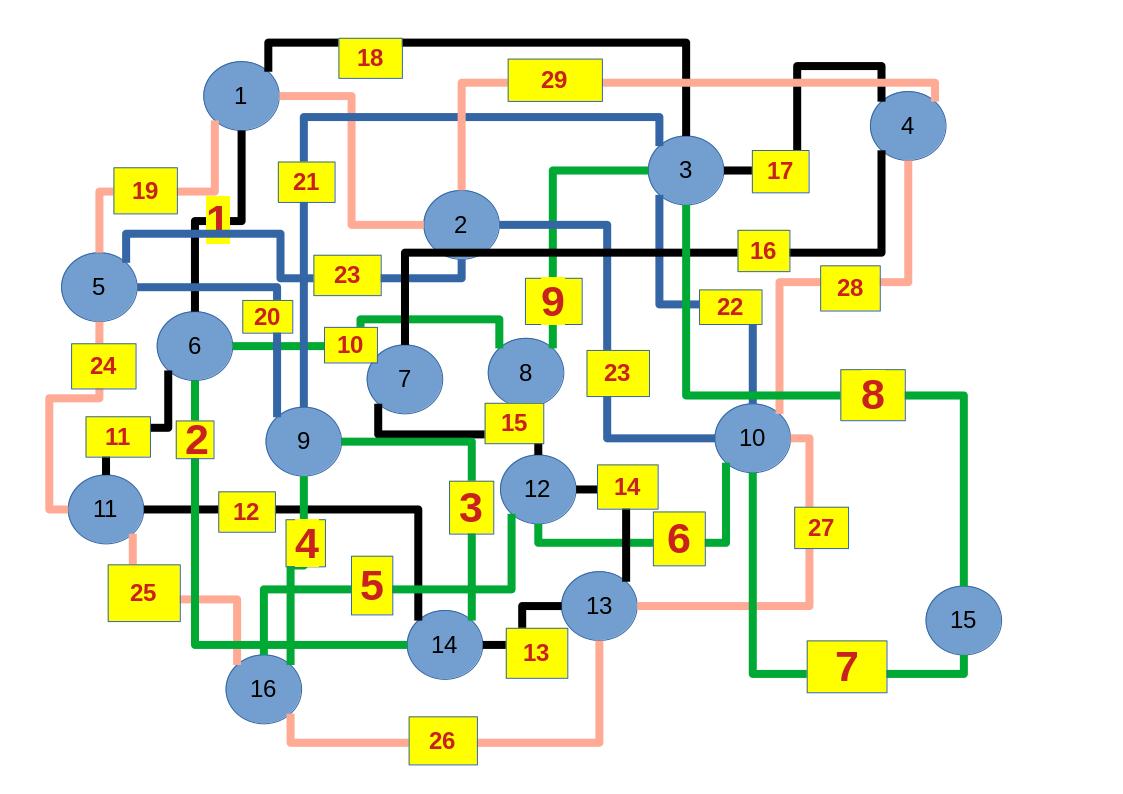
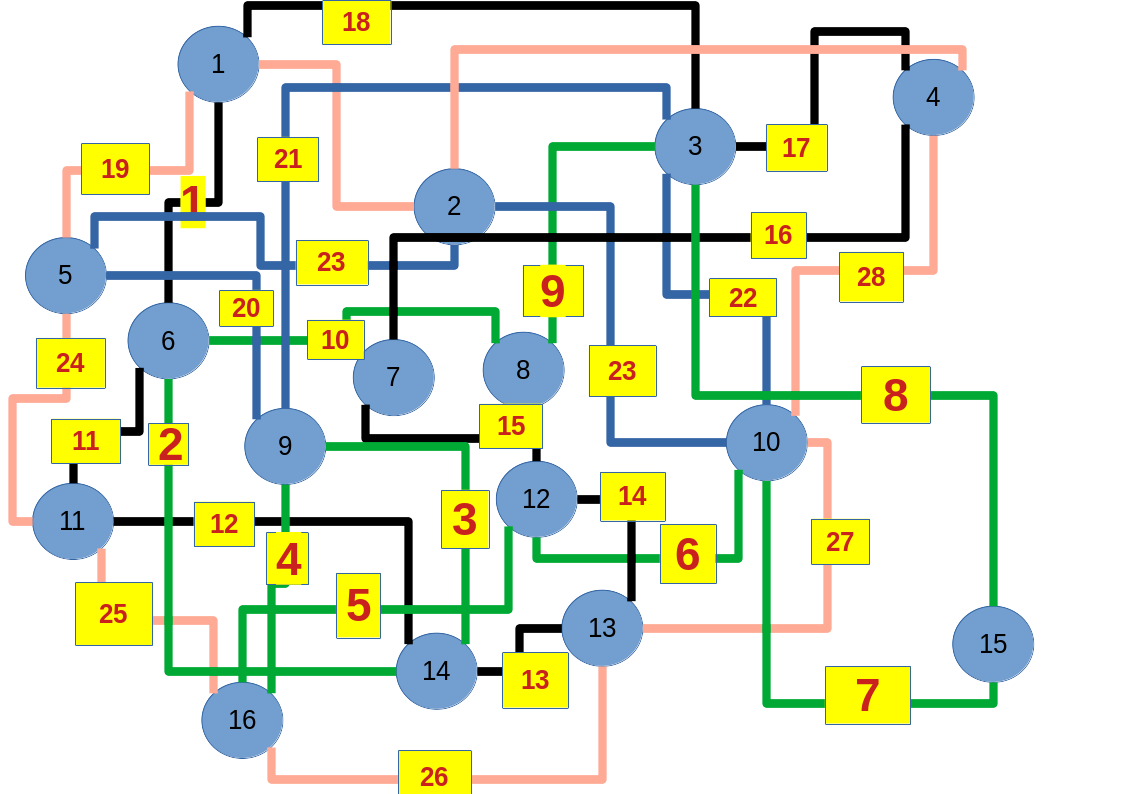
9.) Errechne mit dem Abakus
93 + 57 + 47 + 85 + 52 + 19 + 94 + 84 + 69 + 78


























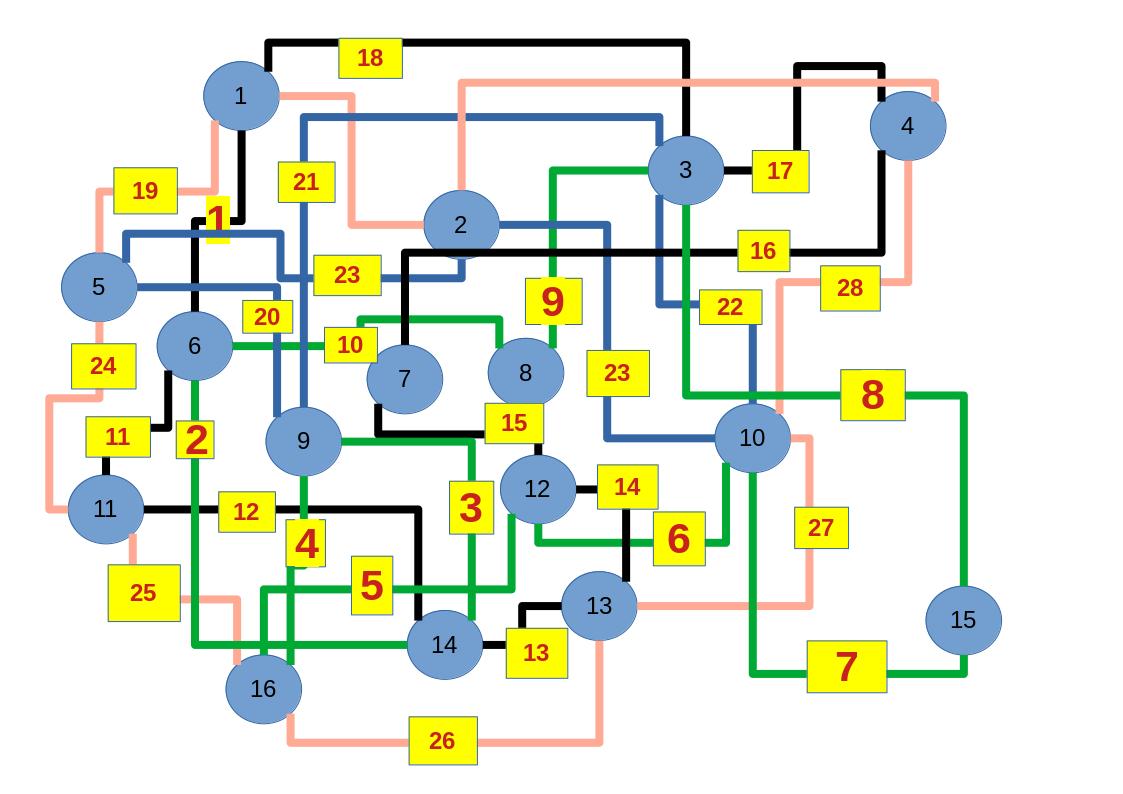
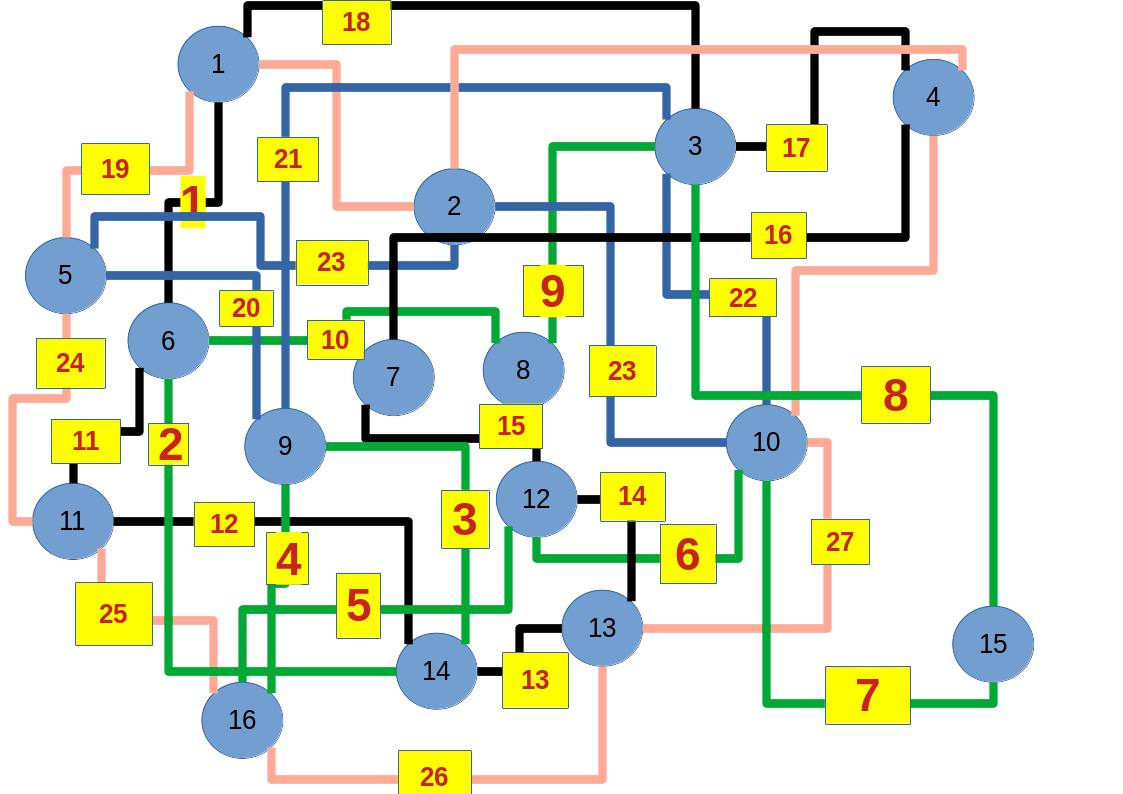
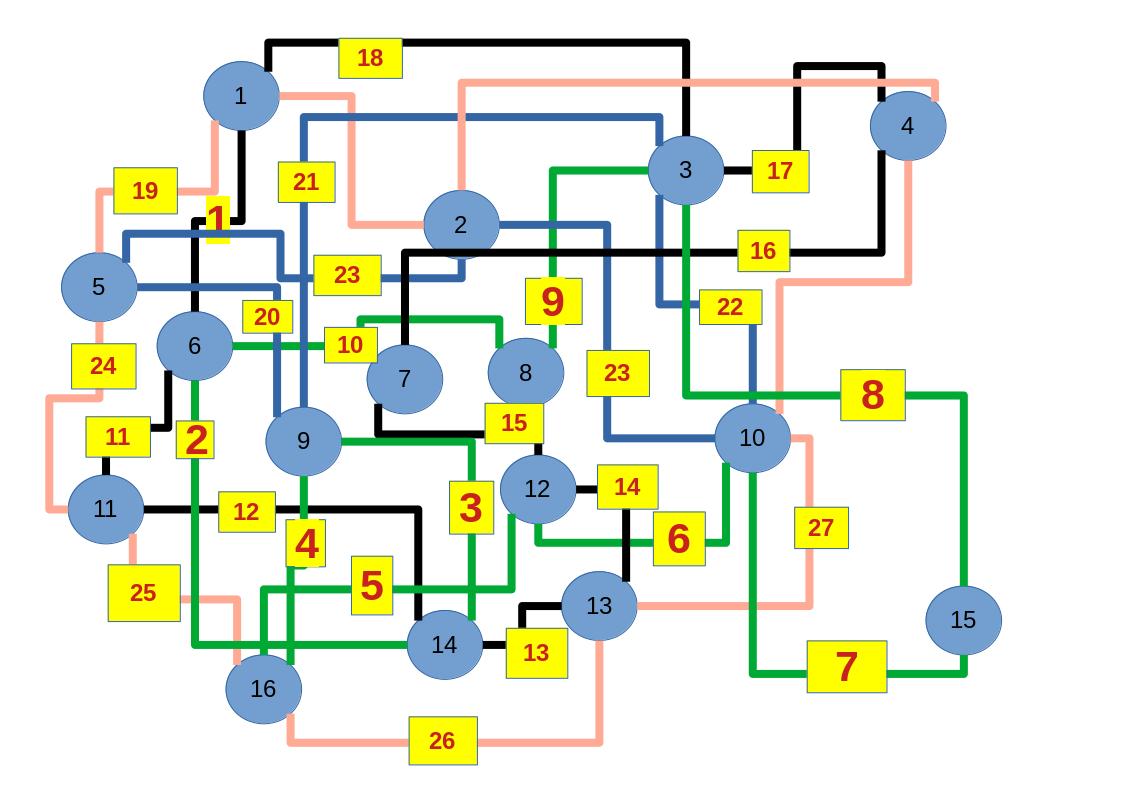
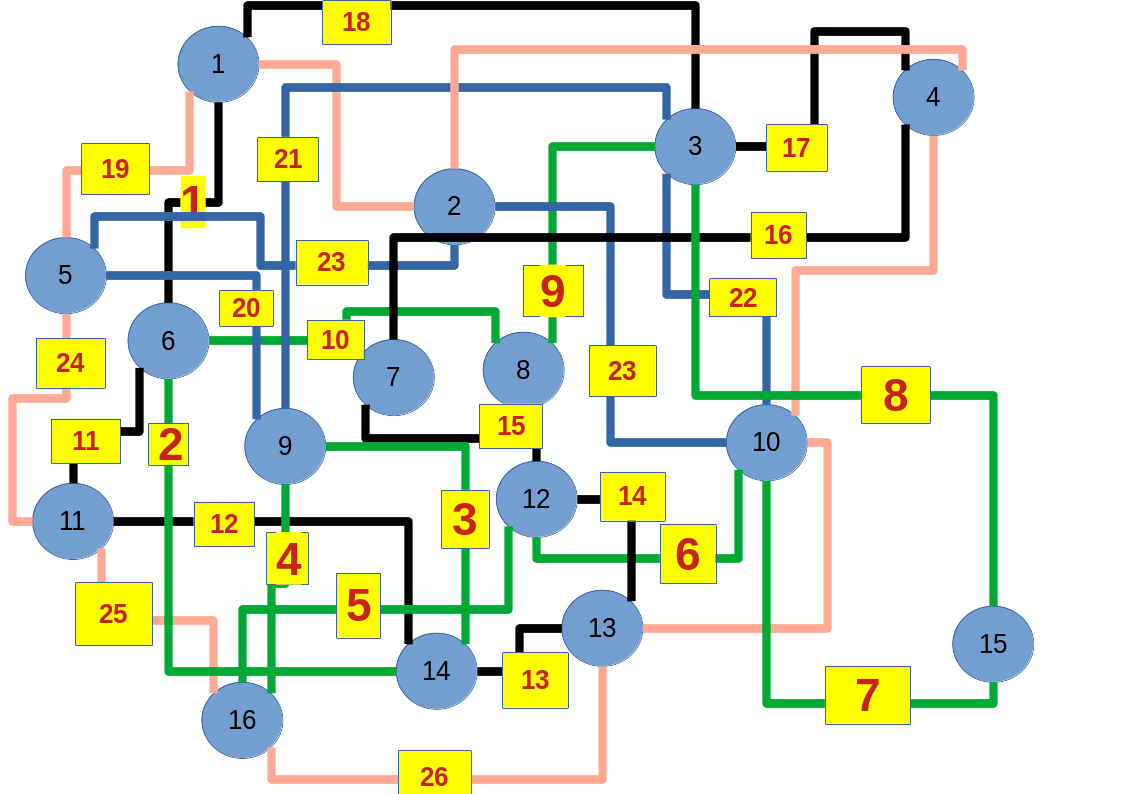
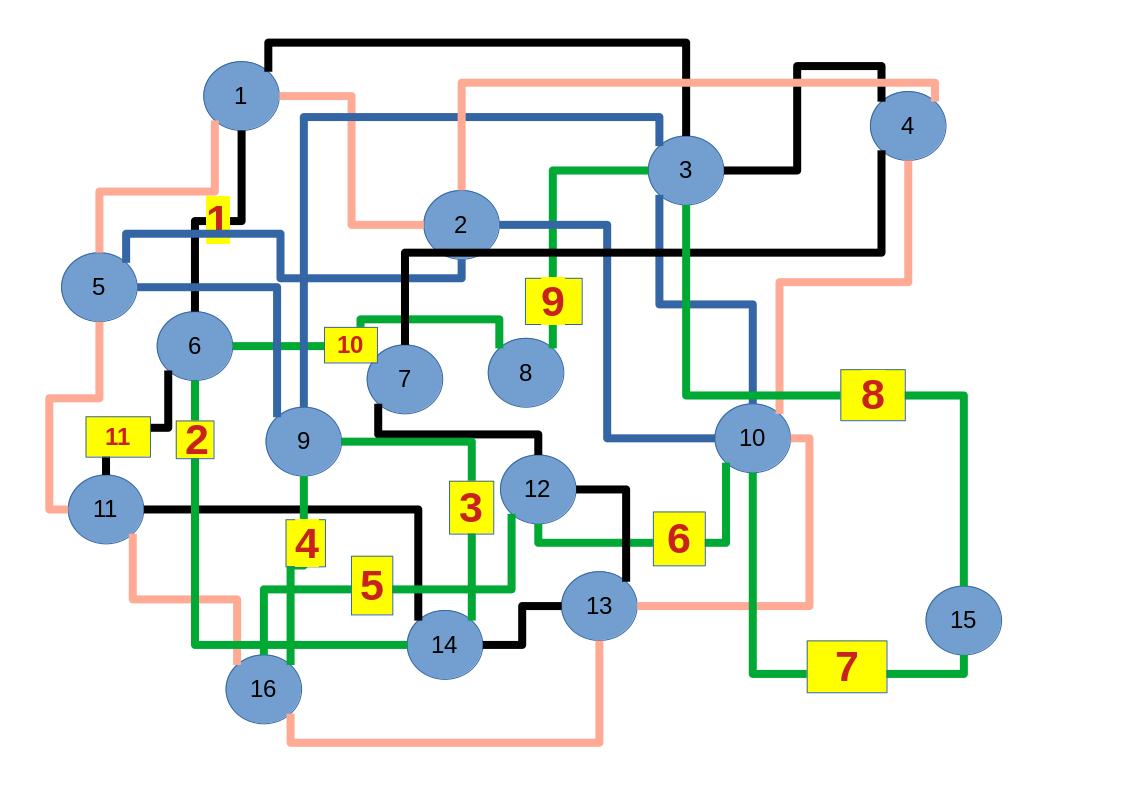
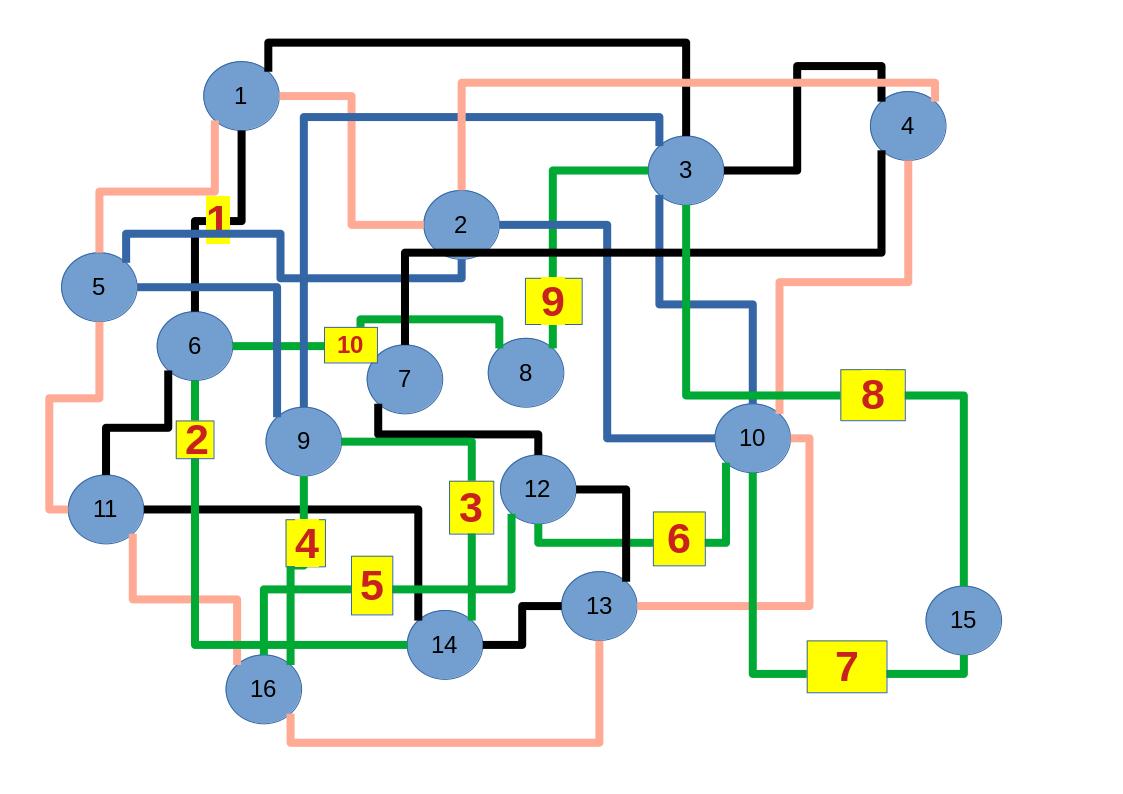
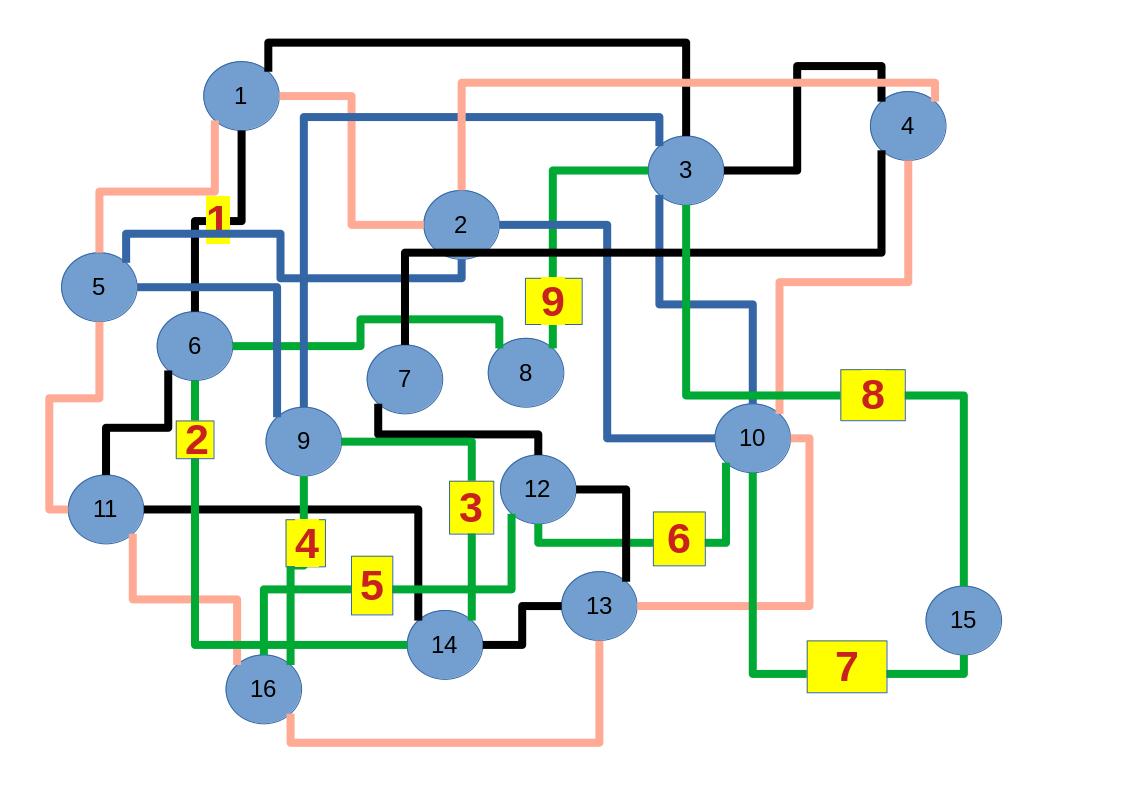
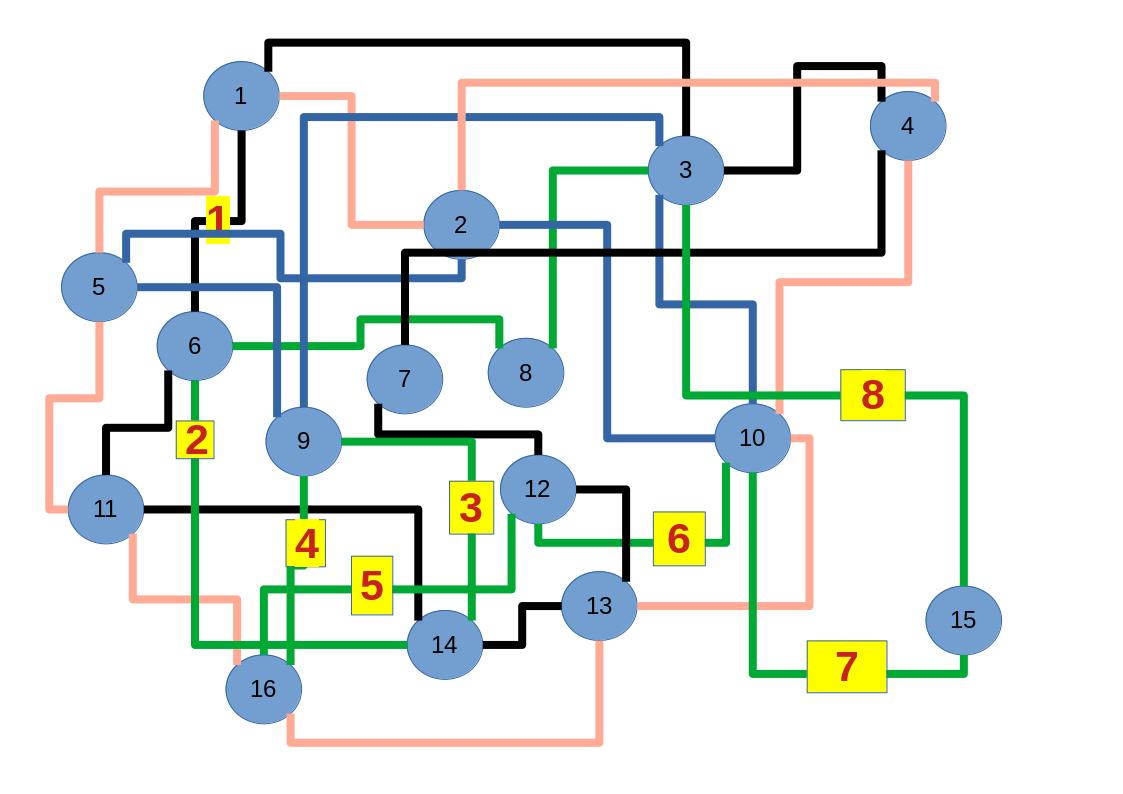
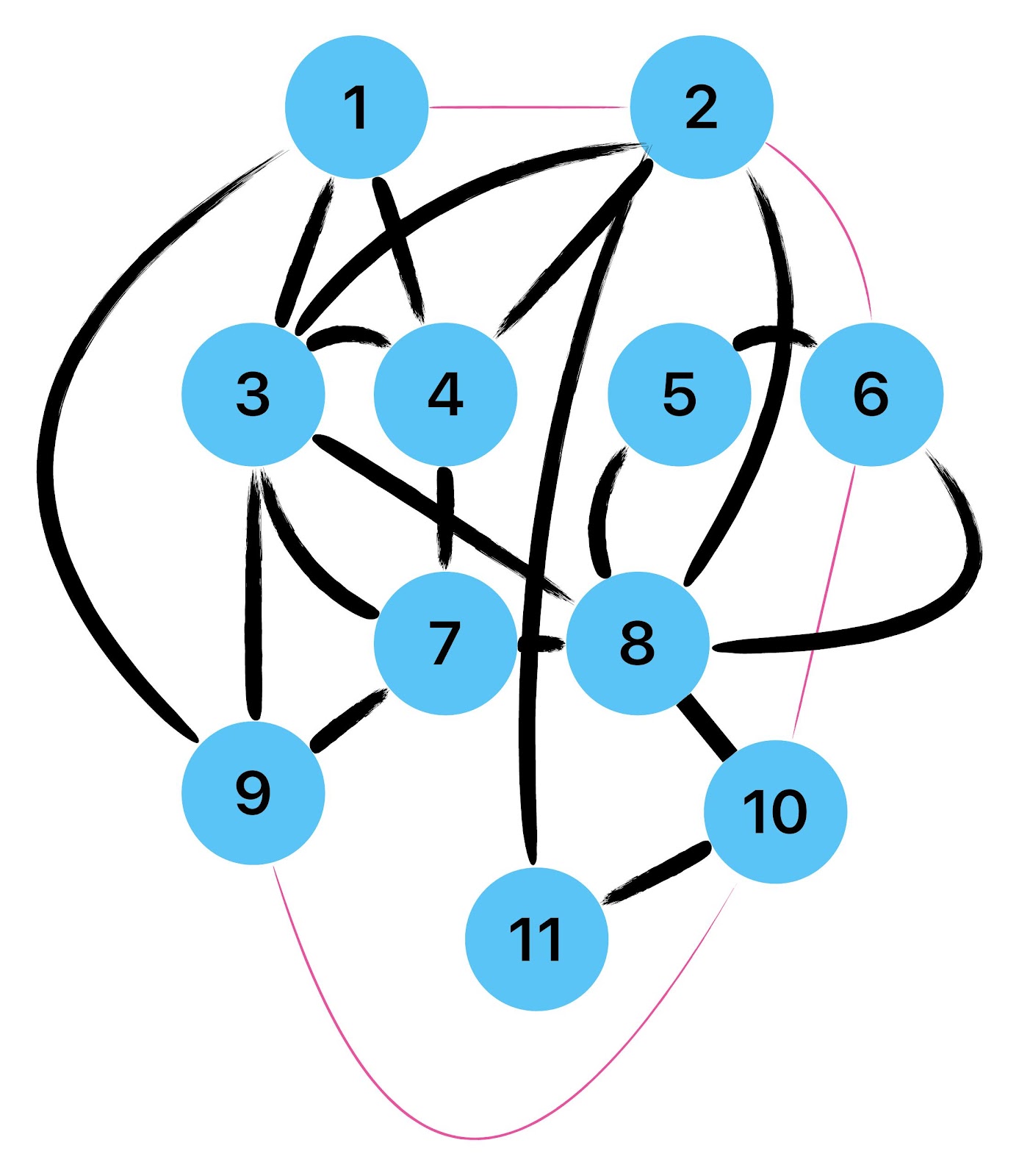
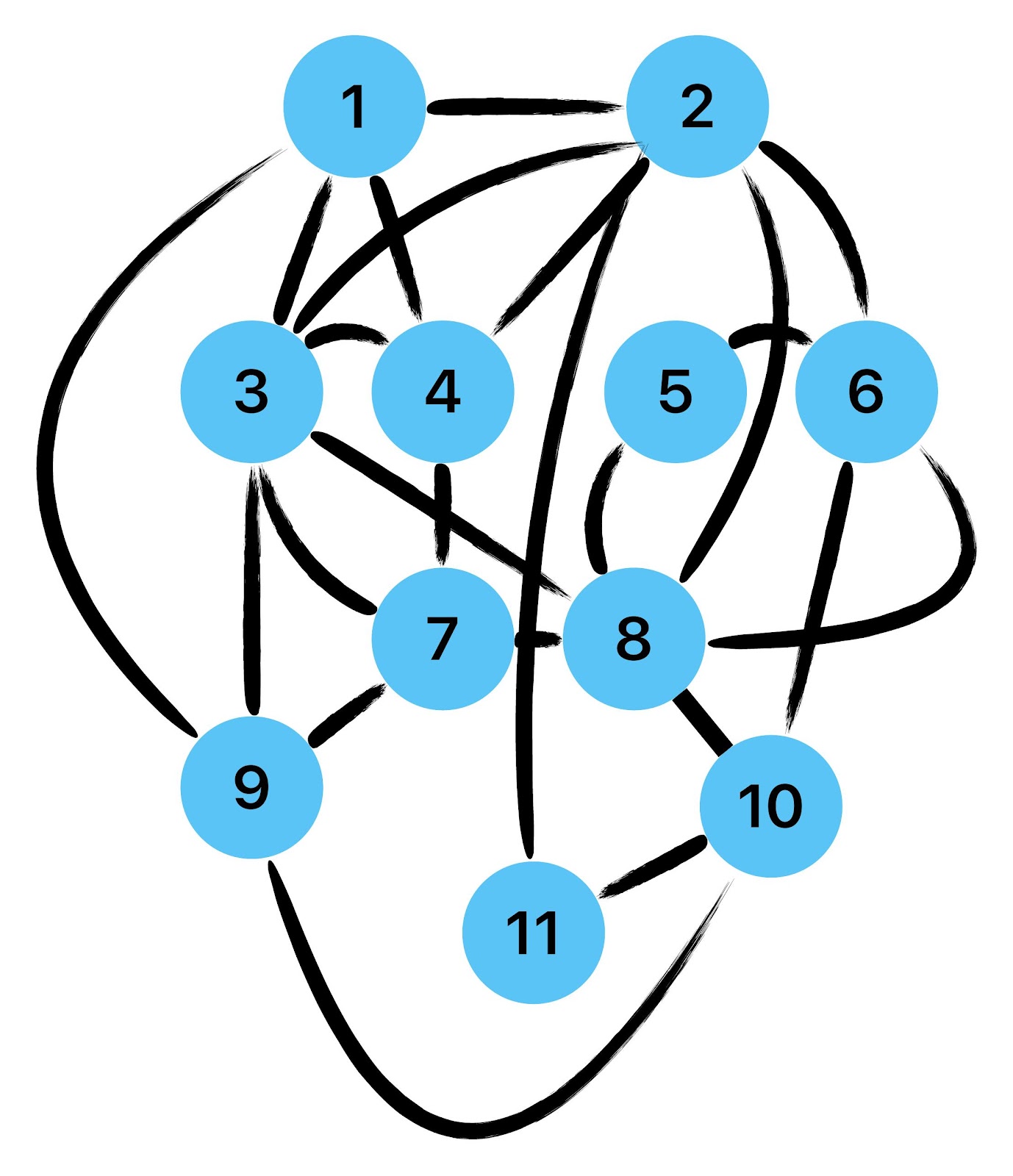
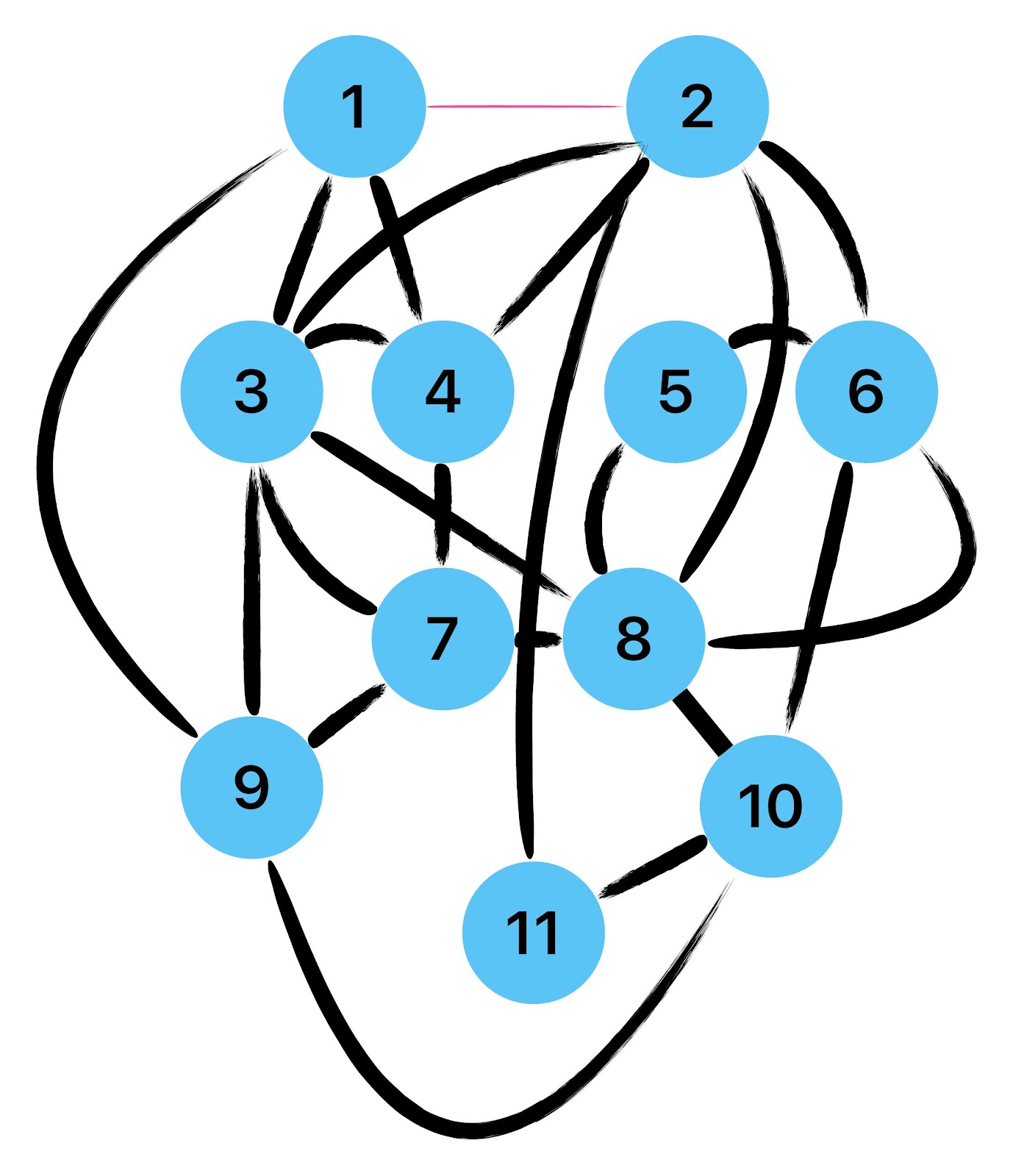
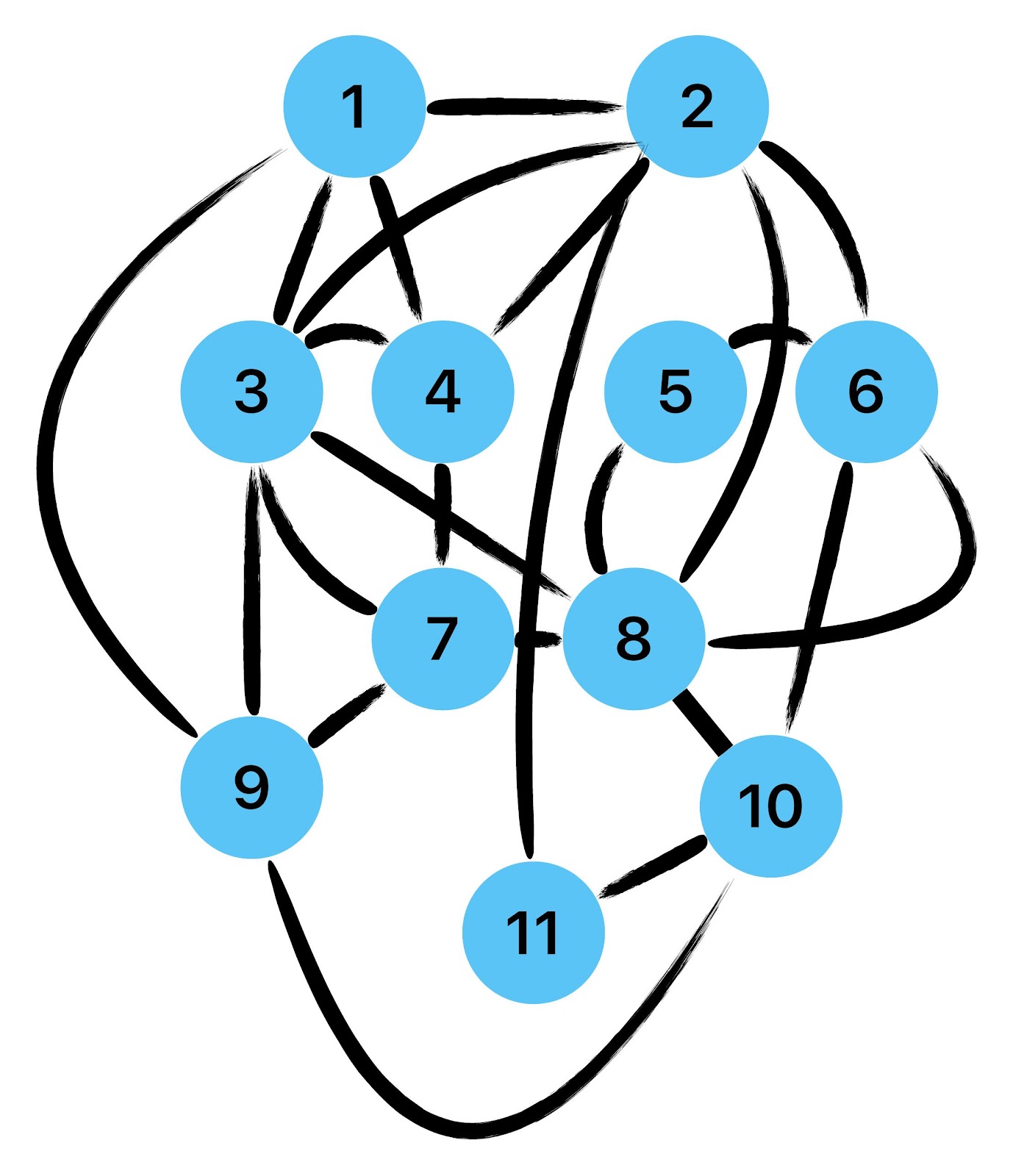
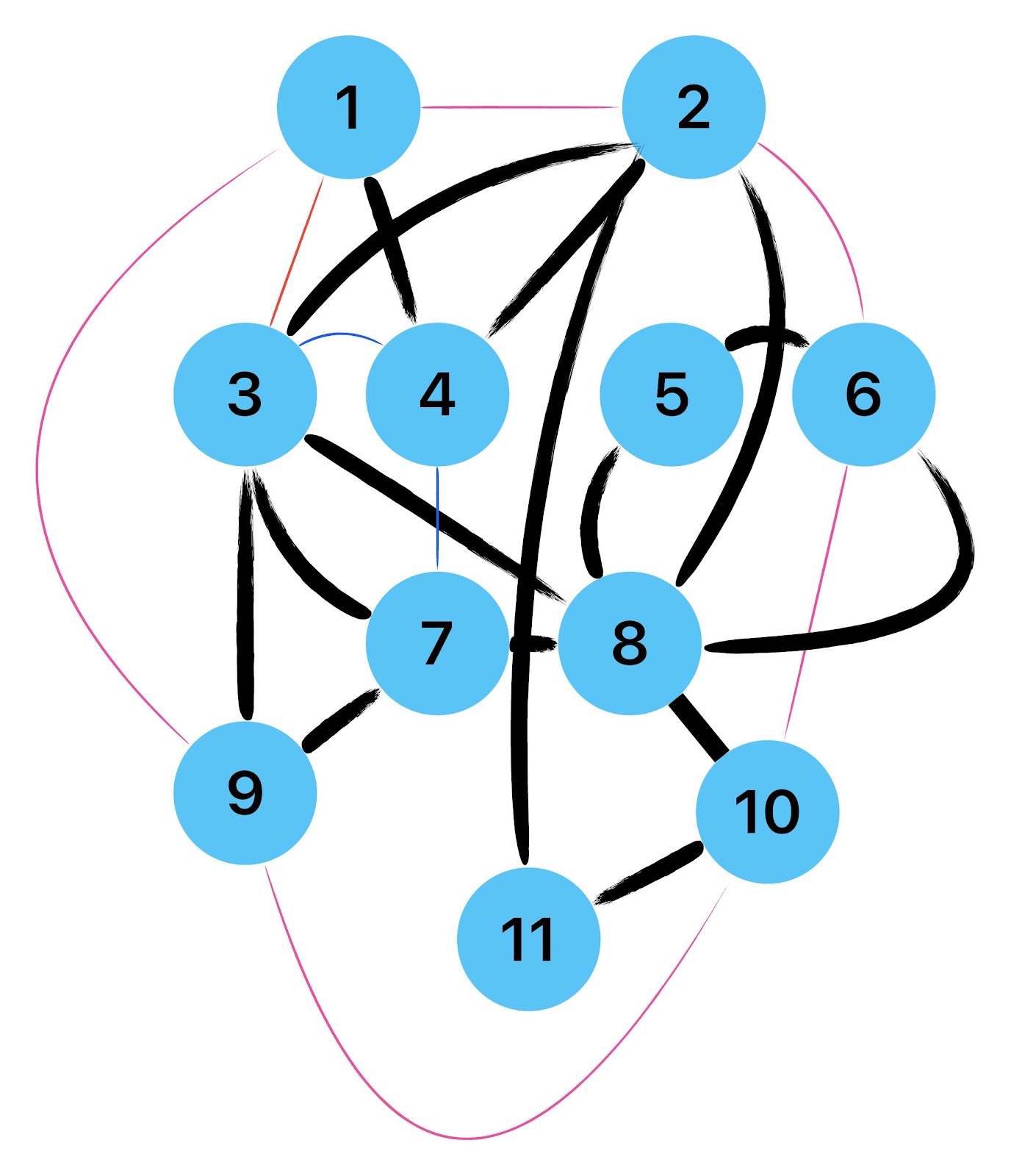
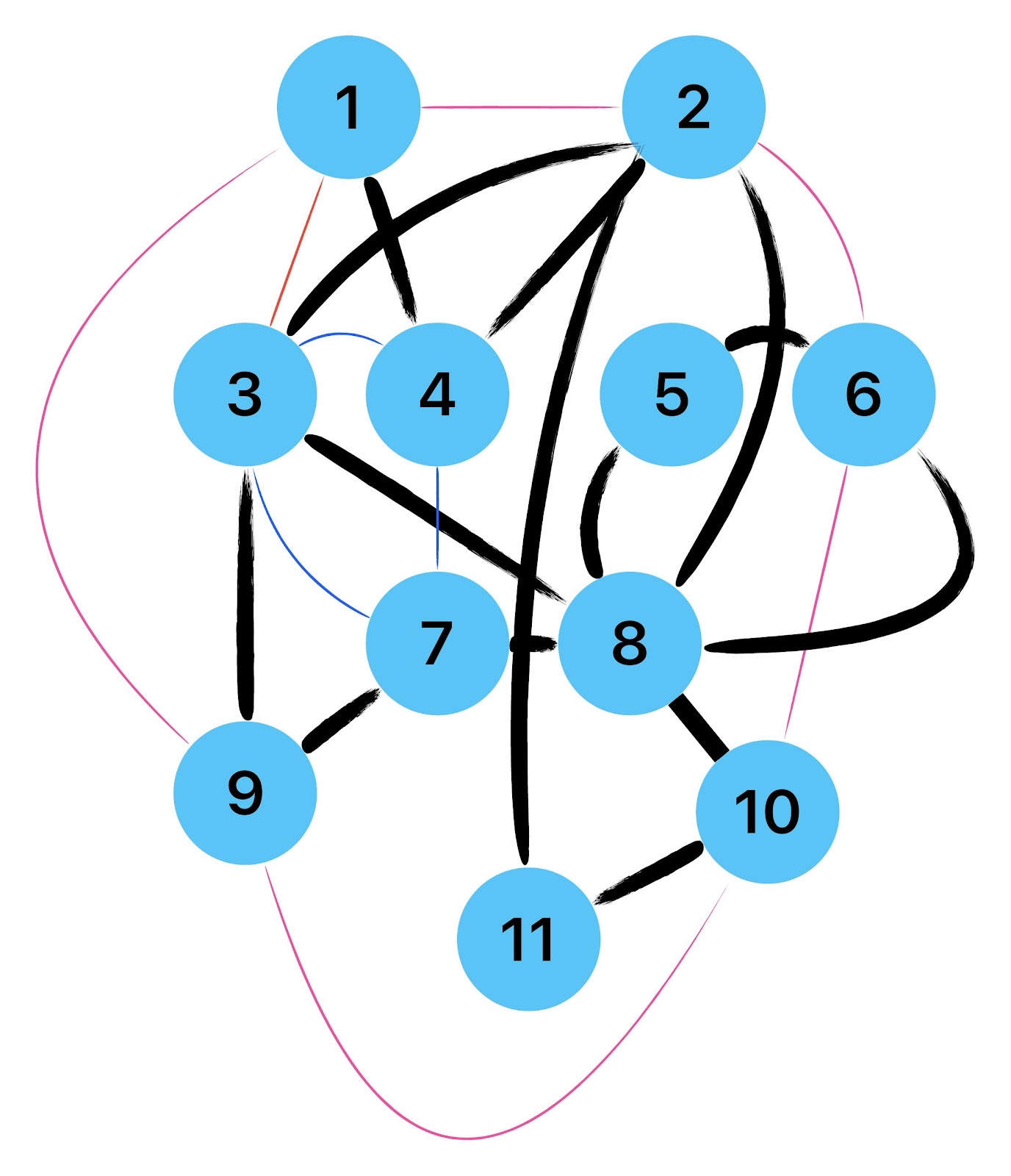
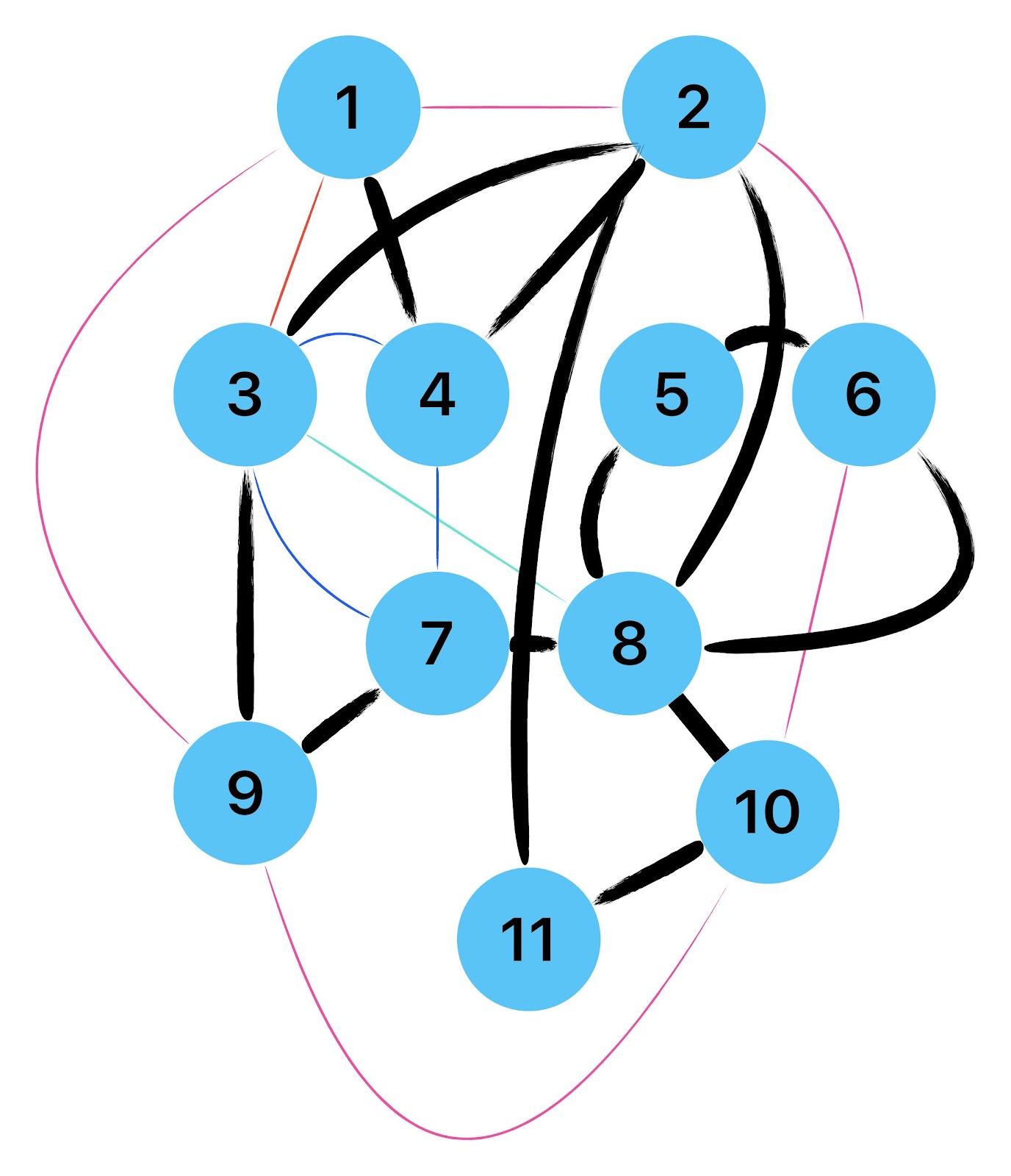
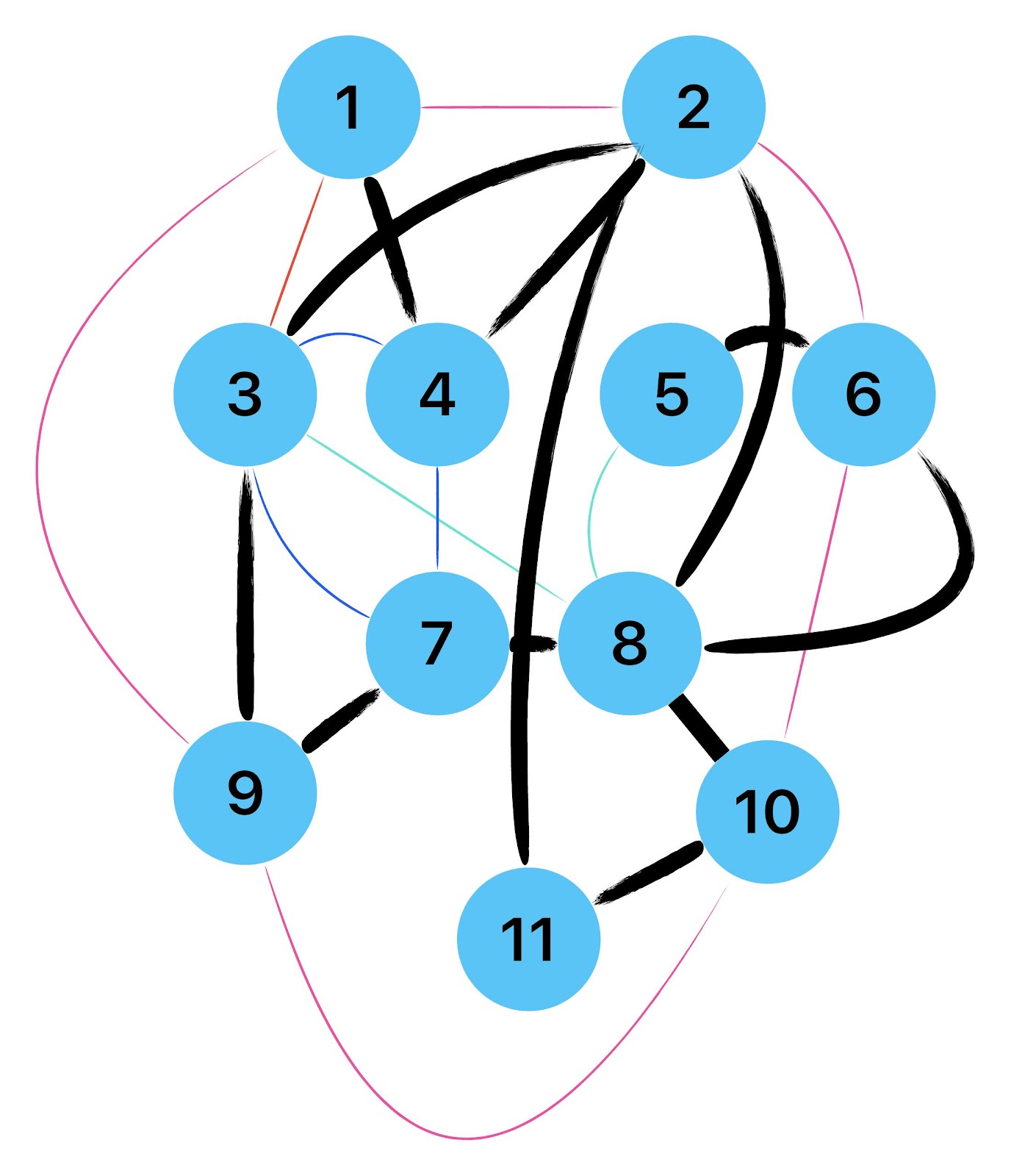
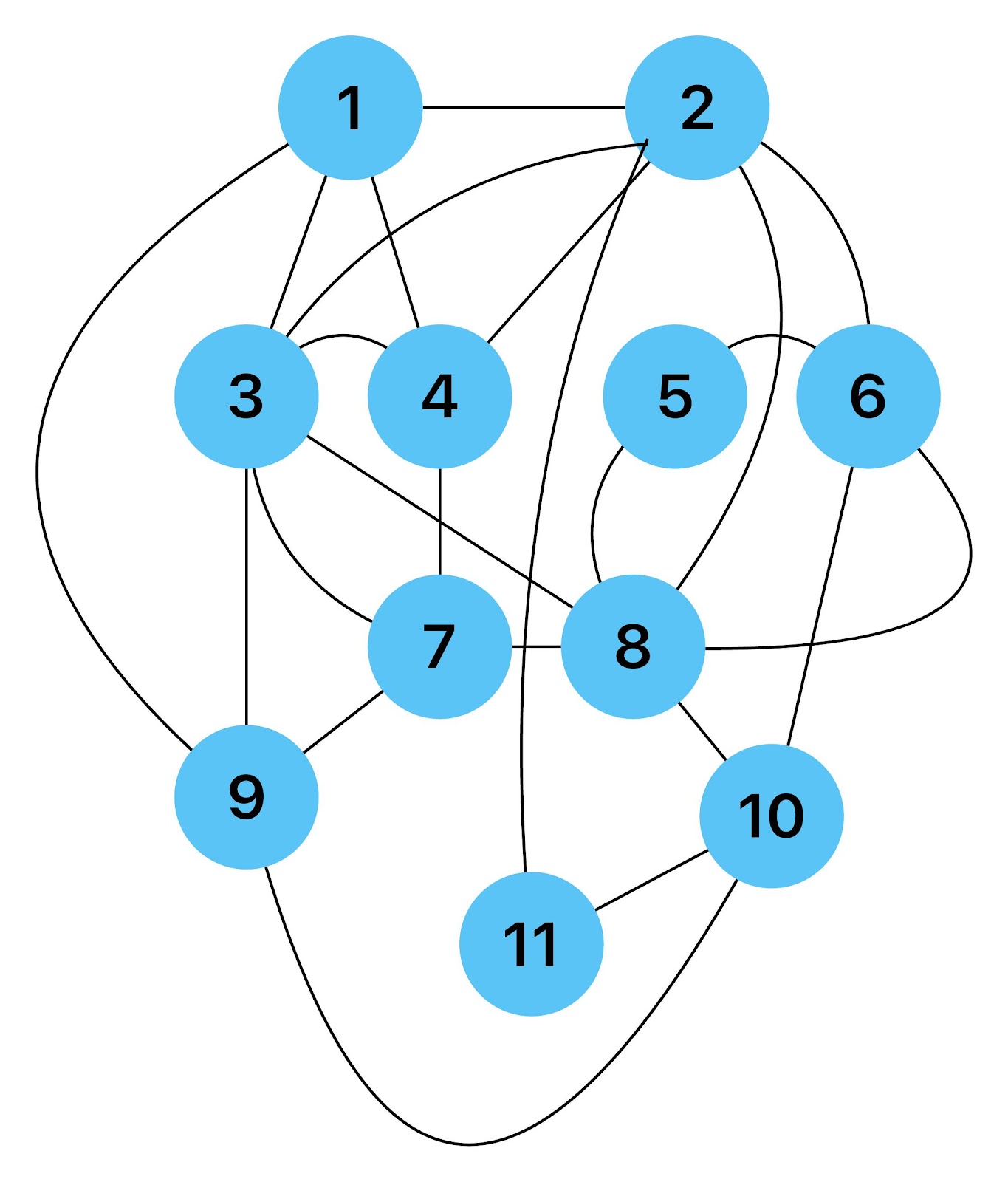
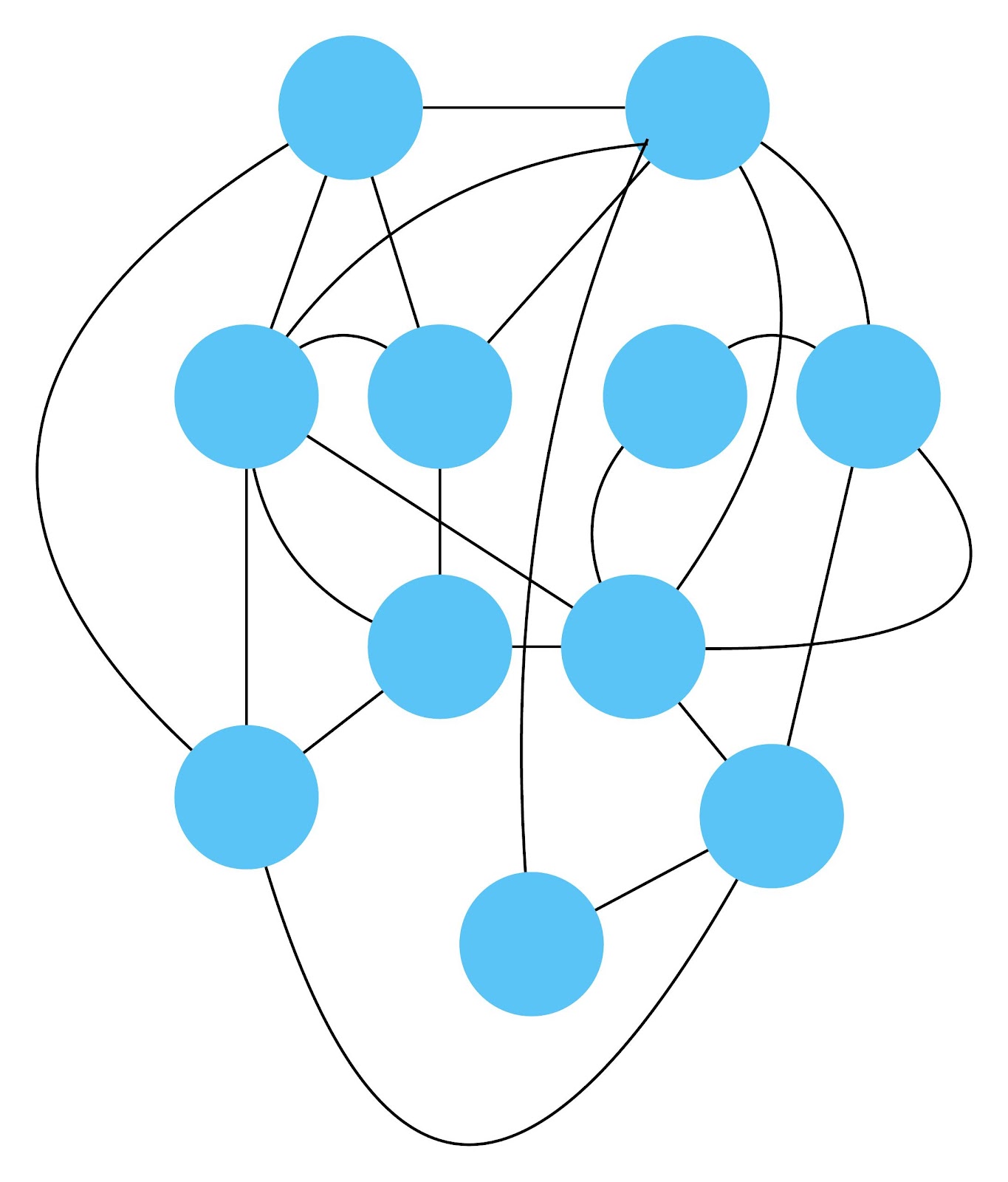
Empfehle auch das hier
Ich lerne auch einfach gleich noch auswendig trotzdem uebe ich Matrizen Operation noch weiter koennen wir sehen es lohnt sich in diesem Fall. Dann haben wir uns sehen funktioniert es auch ganz gut.
Sollen wir dann gleich heute Abend mal bei diesem Thema hier anfangen? Dann fangen wir gleich mal an dann mache ich erst mal die Standard Aufgaben da gehoert diesmal dazu auch die Matrizen Multiplikation halt die ueblichen Aufgaben und die uebliche Rechnen und dann muss ich bei dem Kurs Text was sie mir dafuer Notizen gemacht hat. Am Ende muss ich mir uns besser aufschreiben und dann fange ich mal da noch paar Fehler drin und dann fange ich mal mit dem Text an.
Also jetzt langsam in Ordnung jetzt poste ich erst mal die Sachen die ich hier noch nicht auf Facebook gepostet hab einschliesslich links auf meiner Homepage dann tue ich den Link zu diesem PDF Dings hier auf meine Homepage und dann mache ich die ueblichen Aufgaben mit zusammen mit der Matrizenmultiplikation und wenn ich das hab, dann schreibe ich an meinem Notizen dies zu dem PDF von der Fernuni Hagen habe die Notizen vollstaendig auf und dann melde ich mich mal in diesem Skript zu
So weil Facebook im Theater macht, wenn ich die Links hinterher einfuegen, lass ich das jetzt mal. Jetzt fangen wir an mit den ueblichen Aufgaben d.h. handschriftlich rechnen Abakus und dann kommt noch mal dritte Multiplikation dazu und die uebliche Euler Tour aber mit Papier und halt das uebliche Zeug nur nix nichts mathematisches und dann schreibe ich das was bei dem Skript bei mir noch nicht stimmt bei dir Notizen von der Fernuni Hagen raus und dann wende ich mich mal dem dazu aber neues auf jeden Fall die Matrizenmultiplikation, die auf jeden Fall sitzen muss
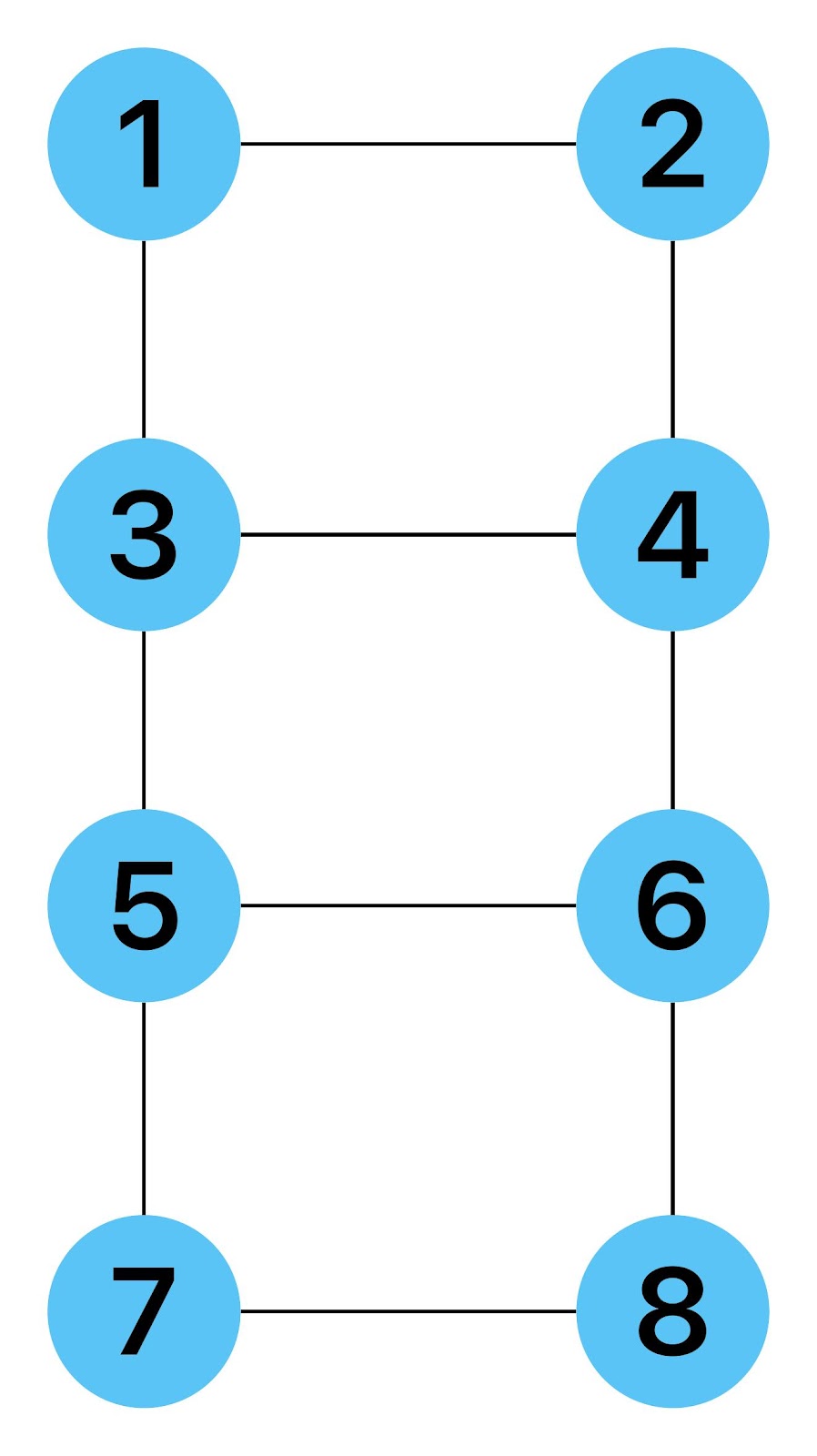
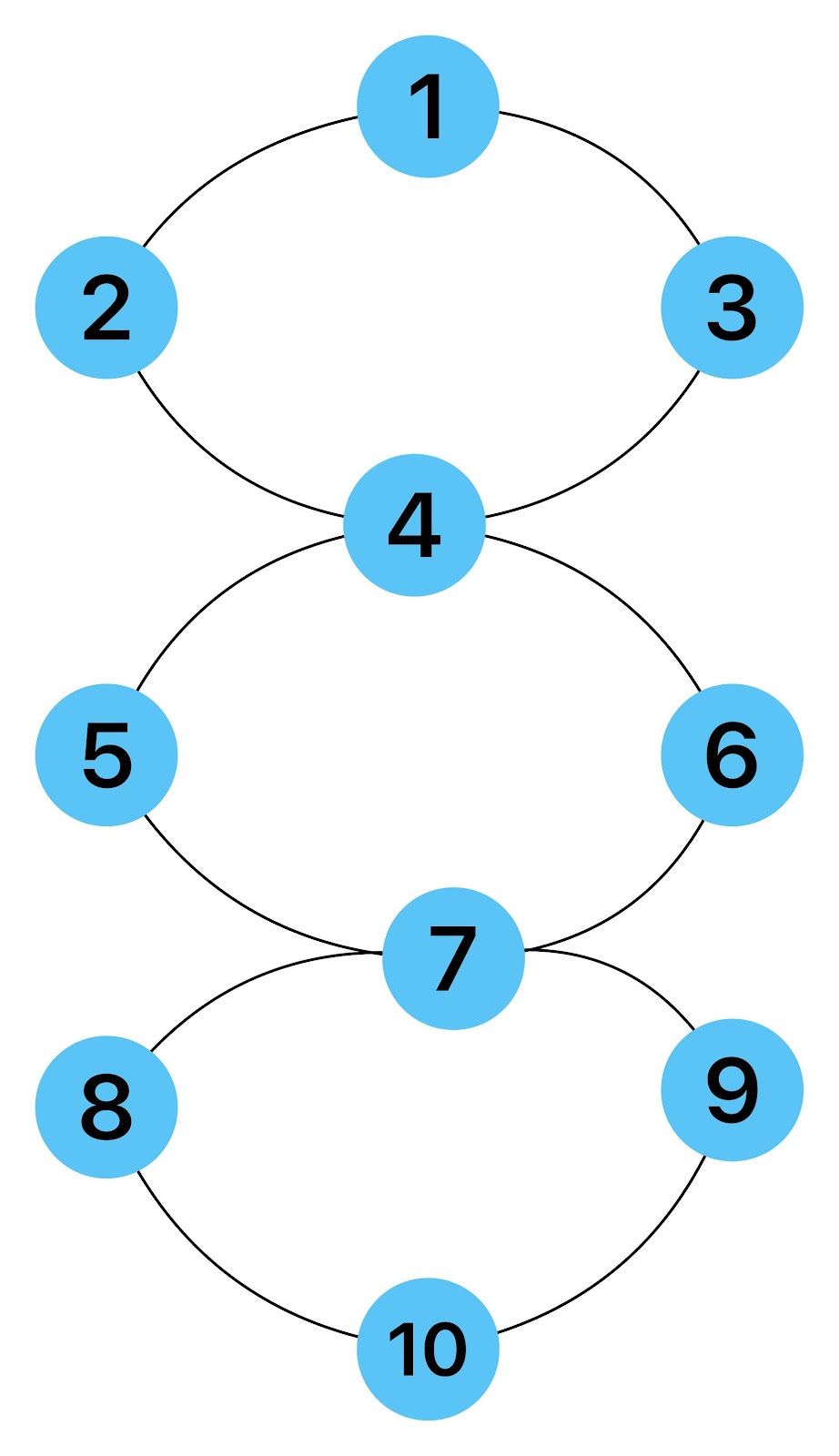
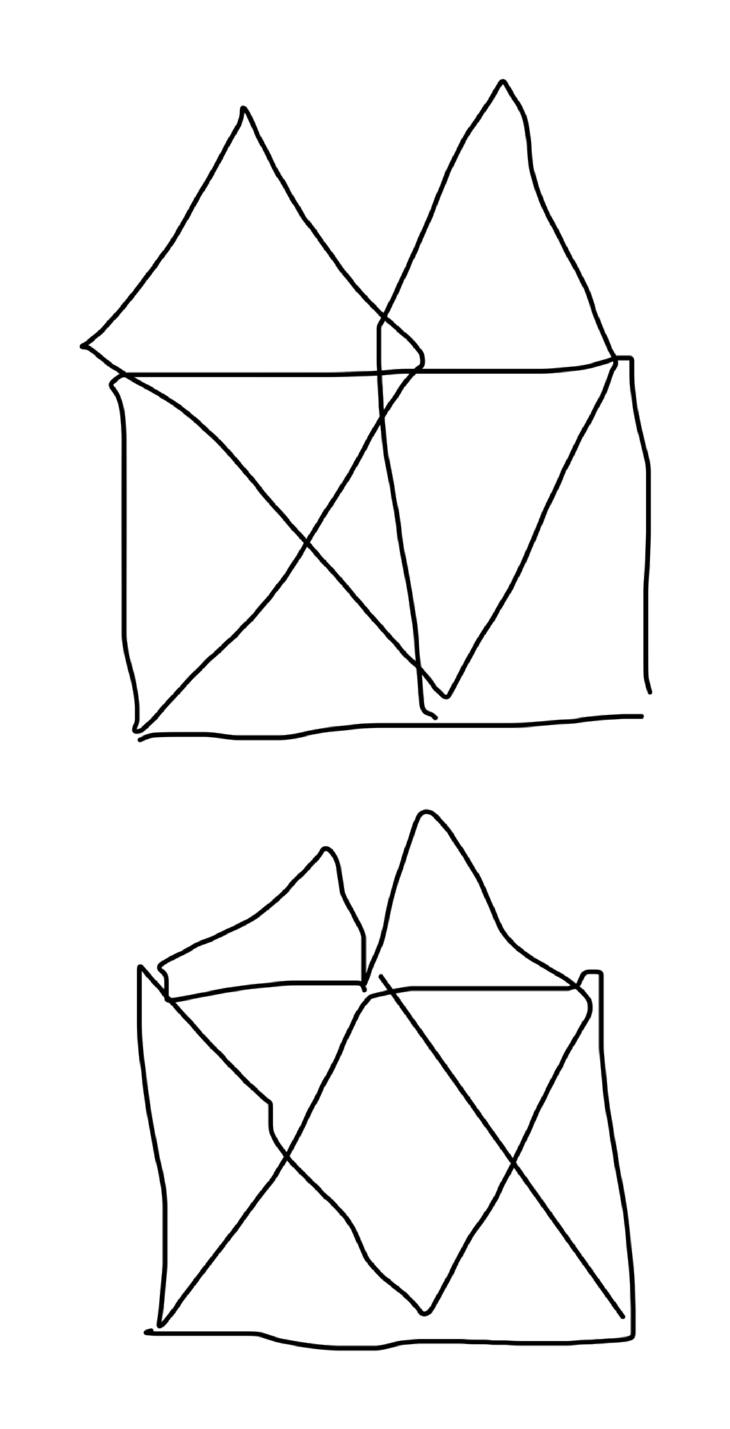
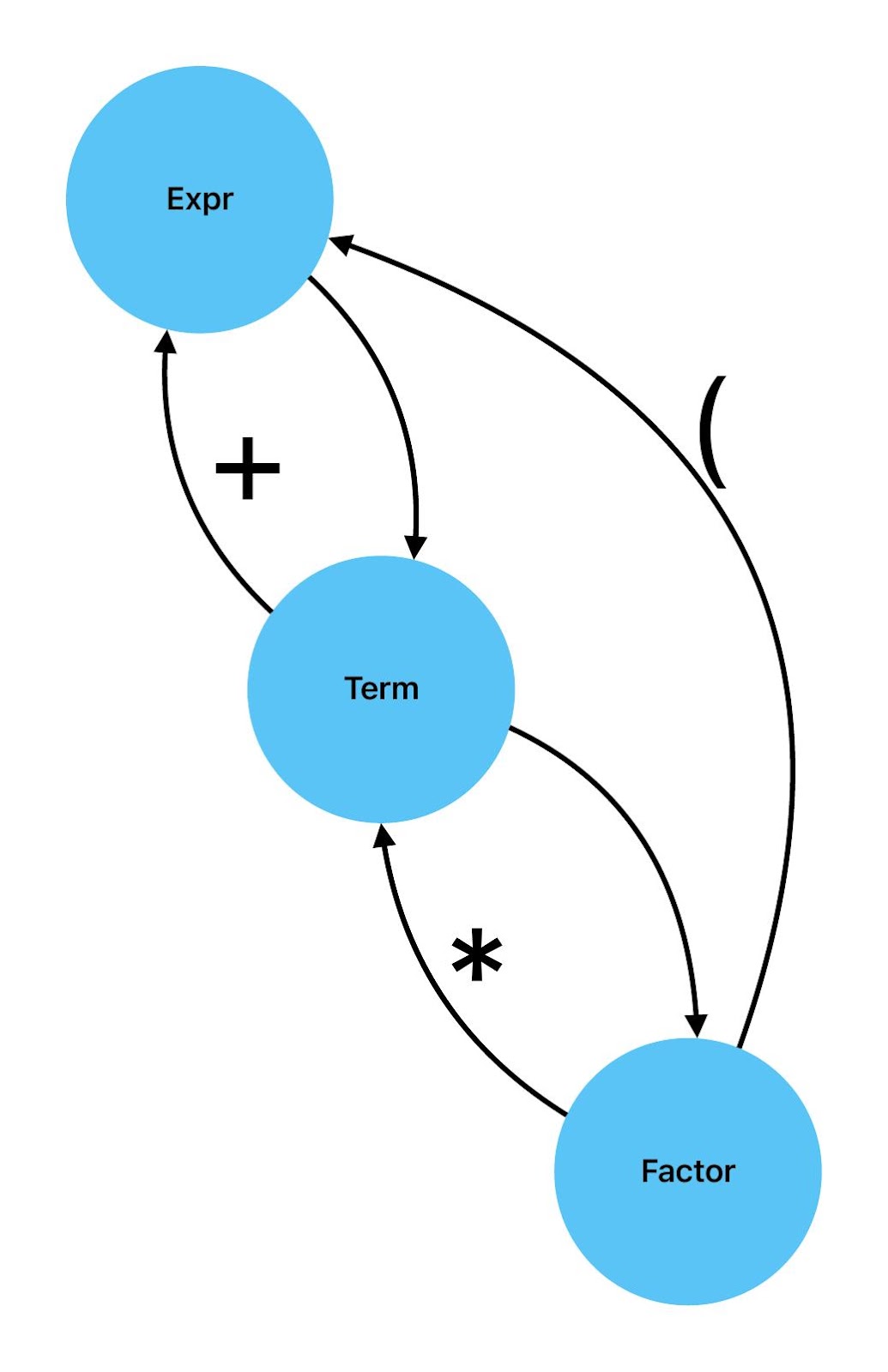
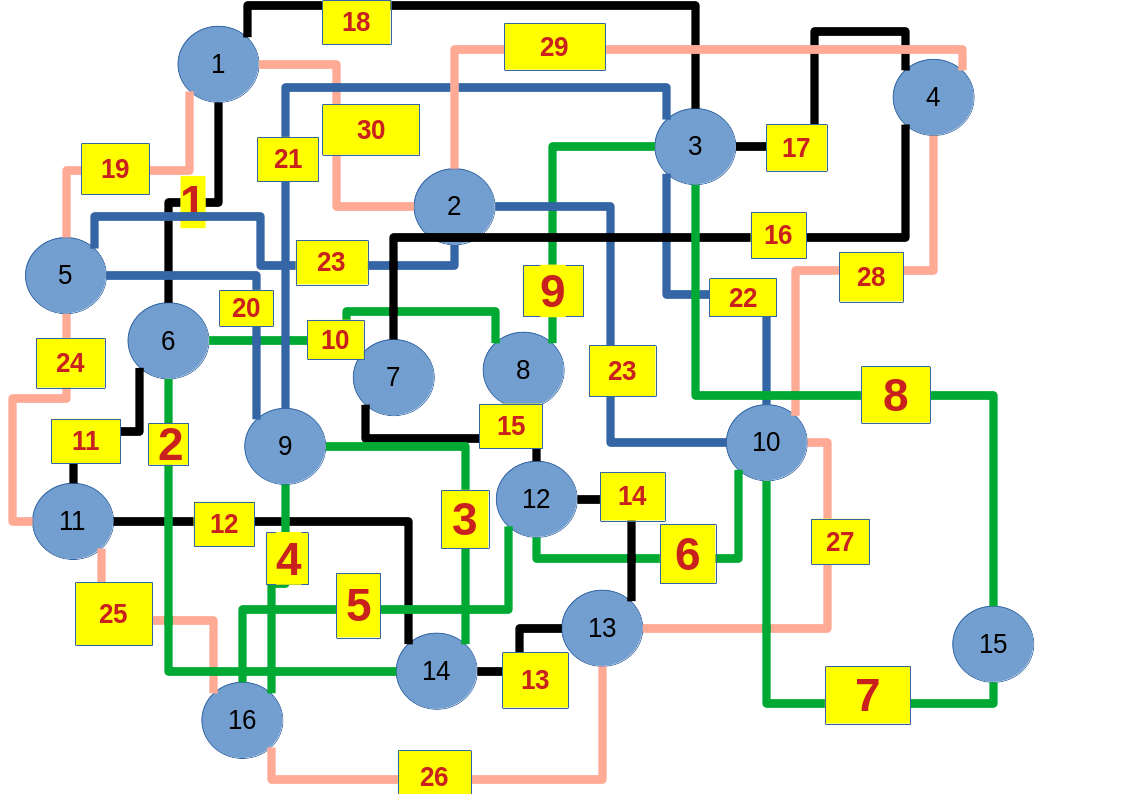
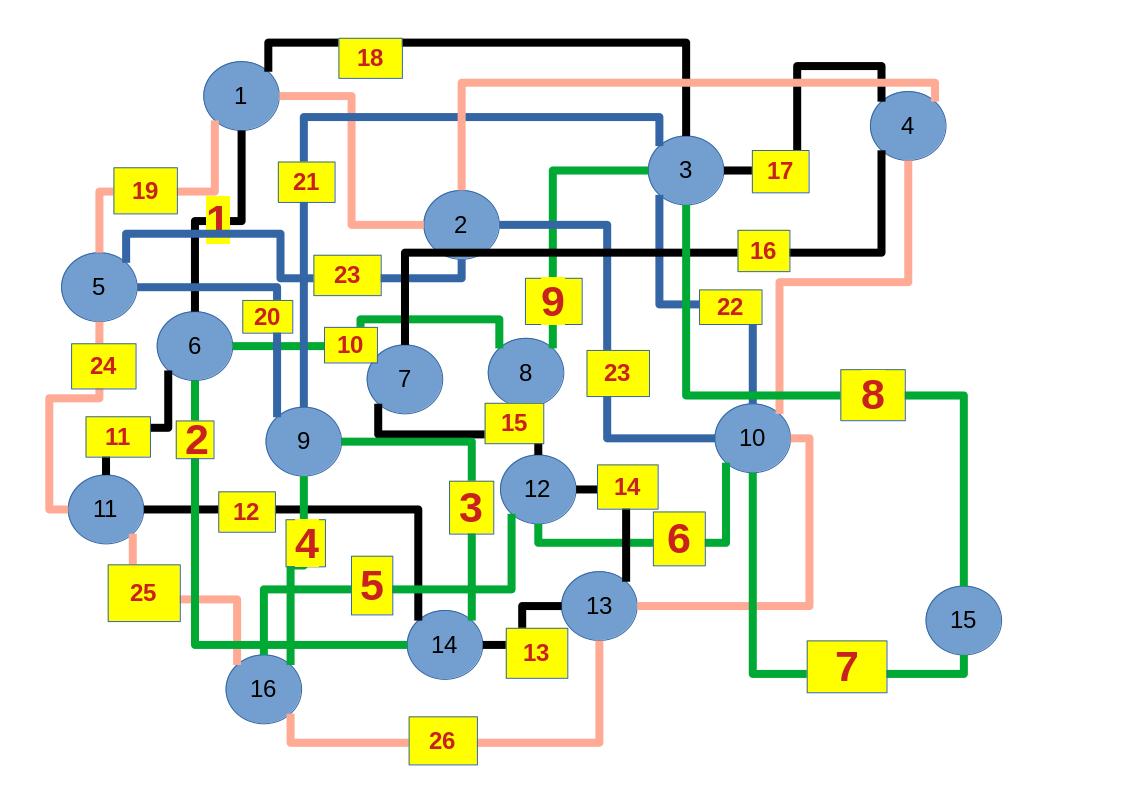
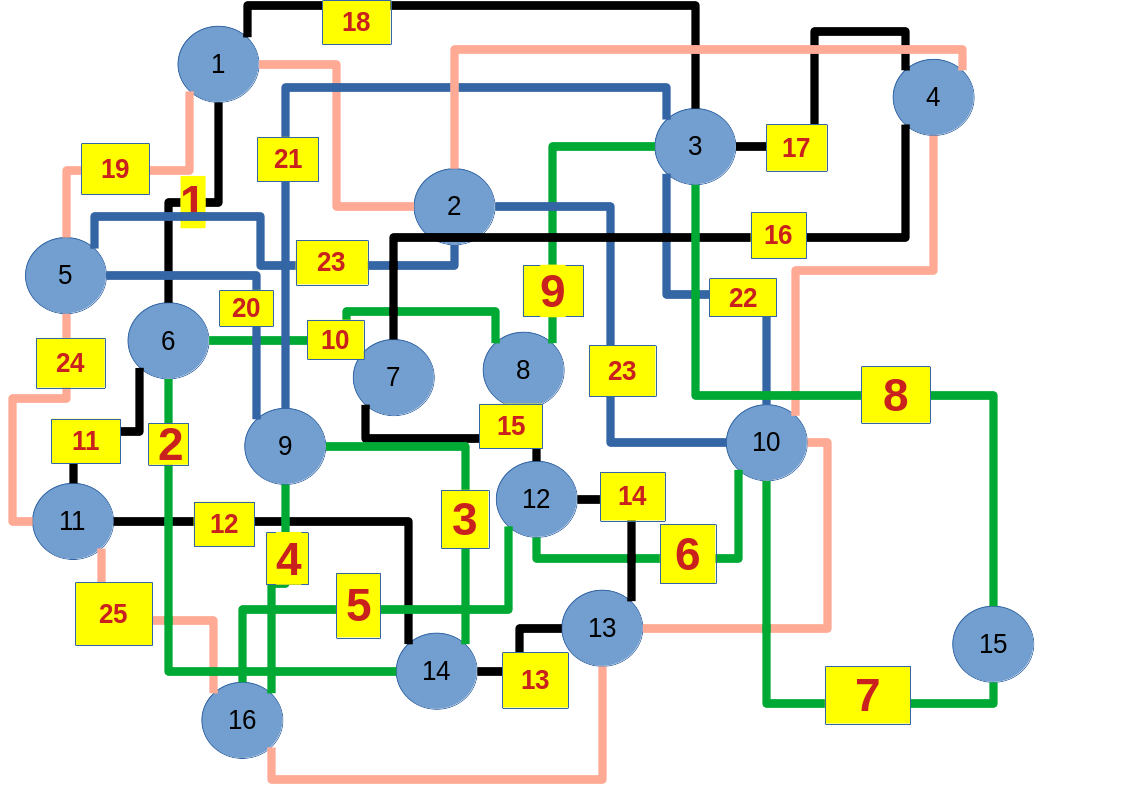
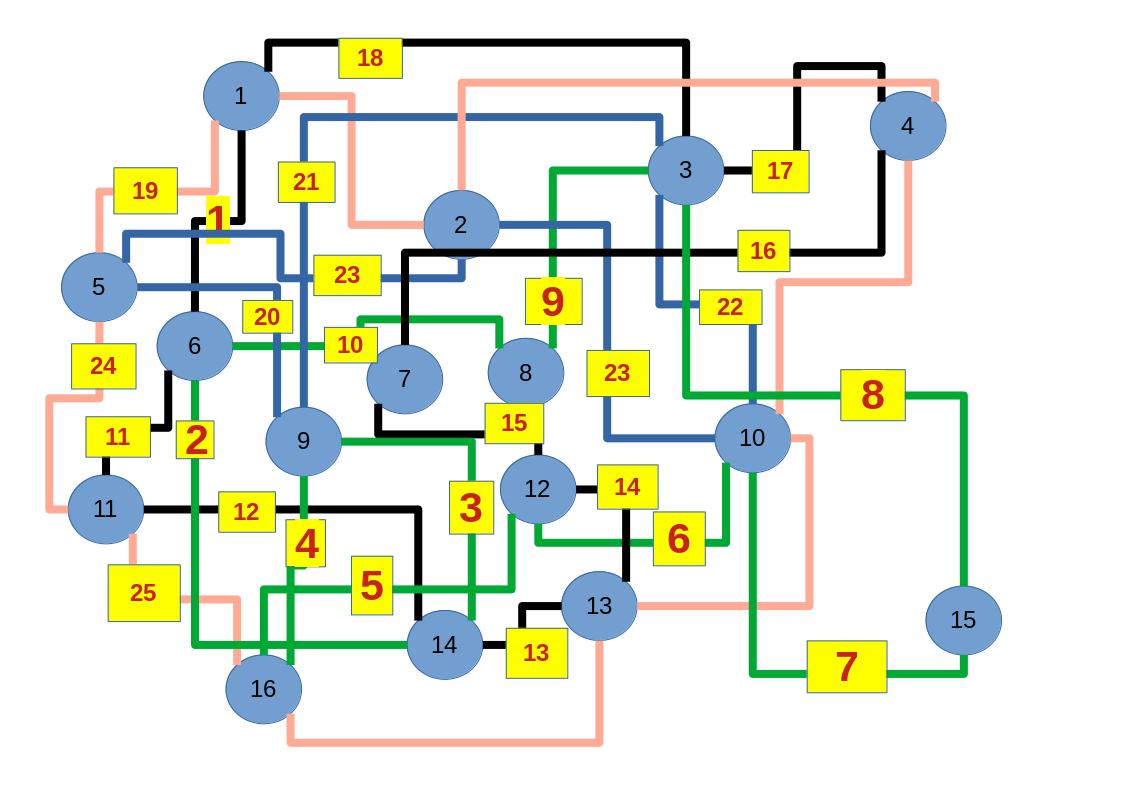
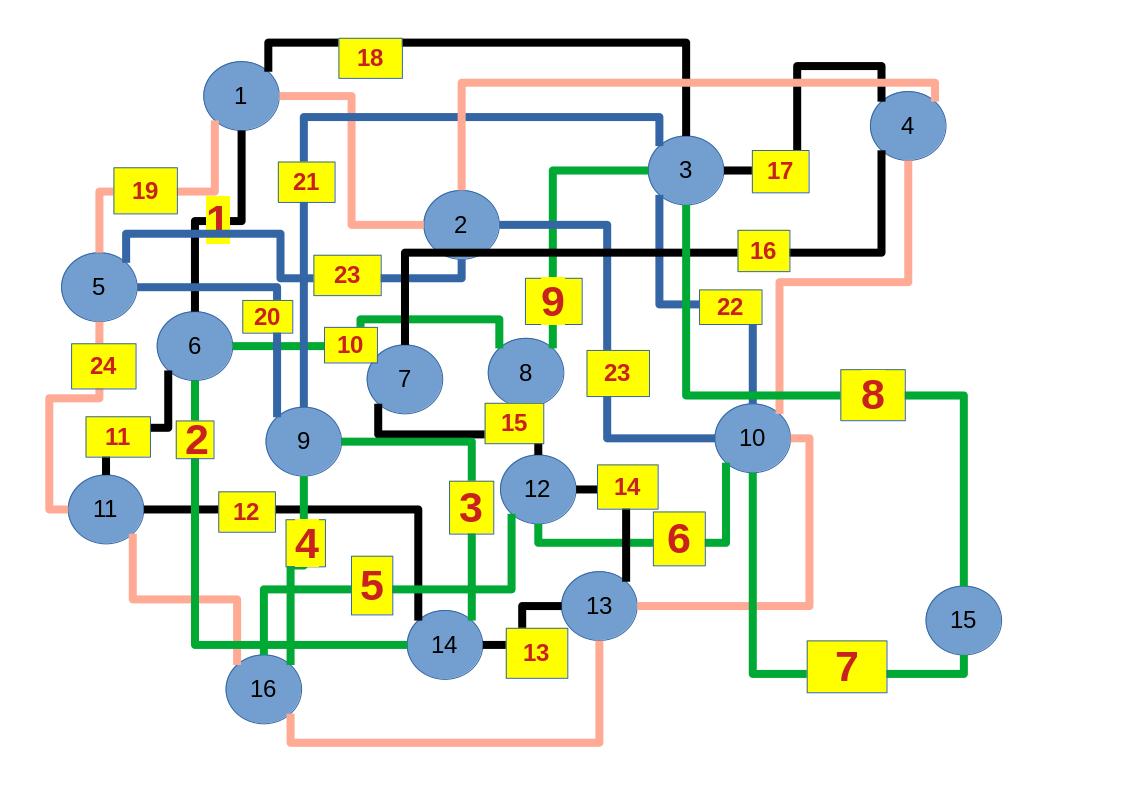
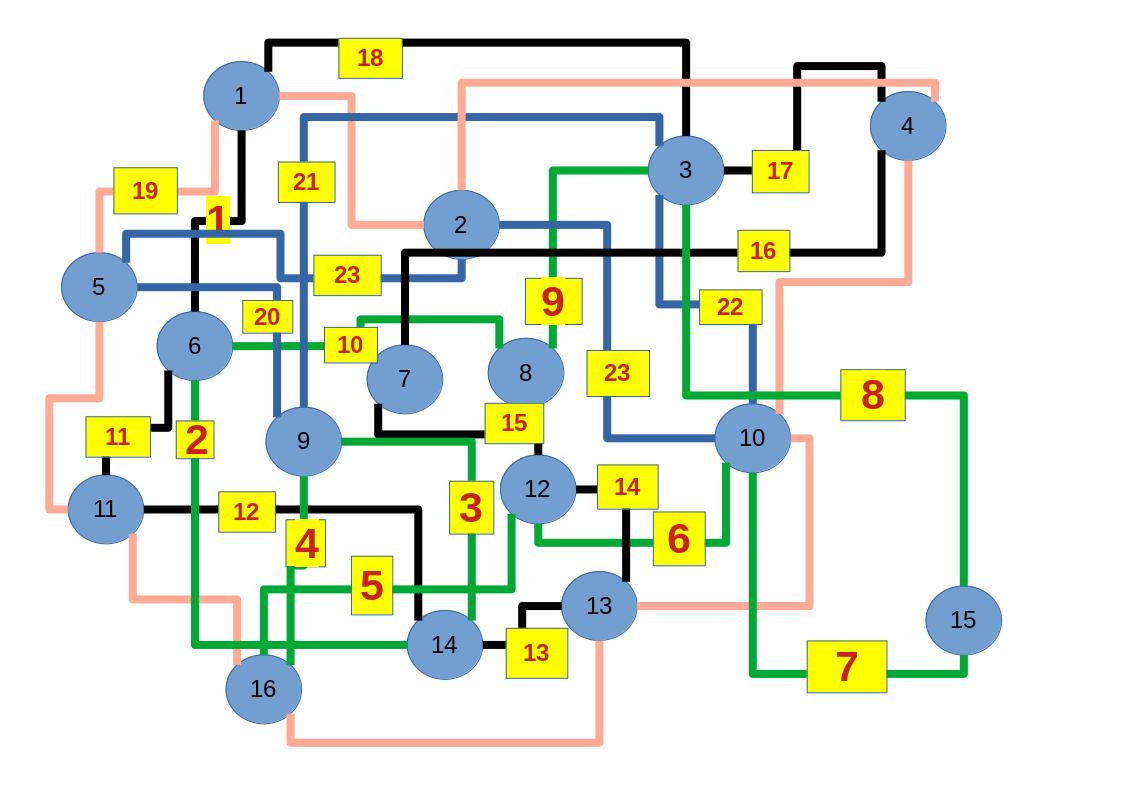
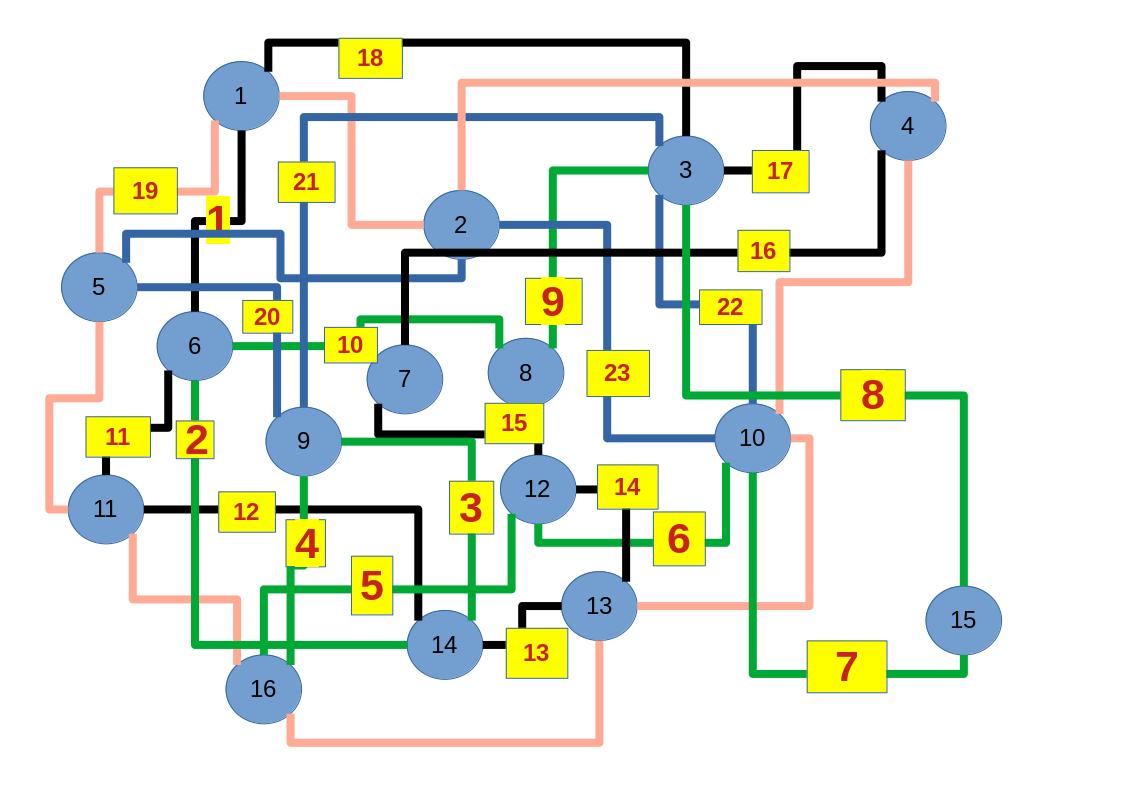
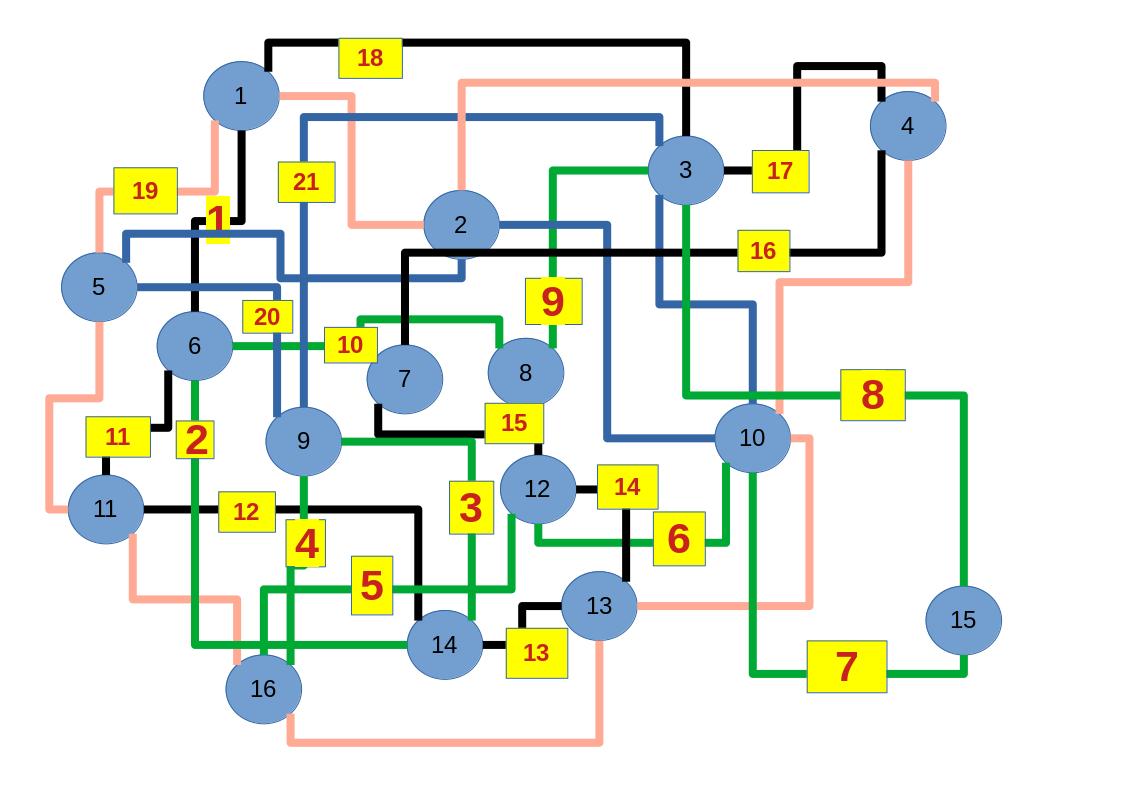
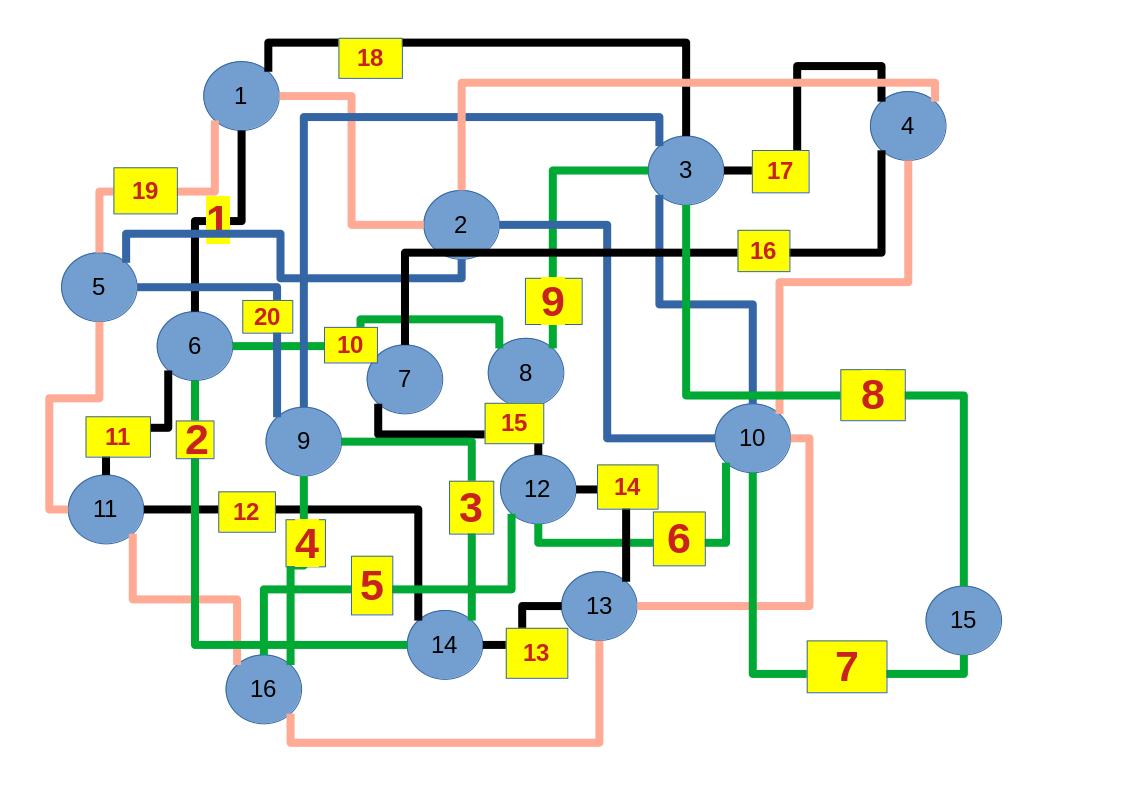
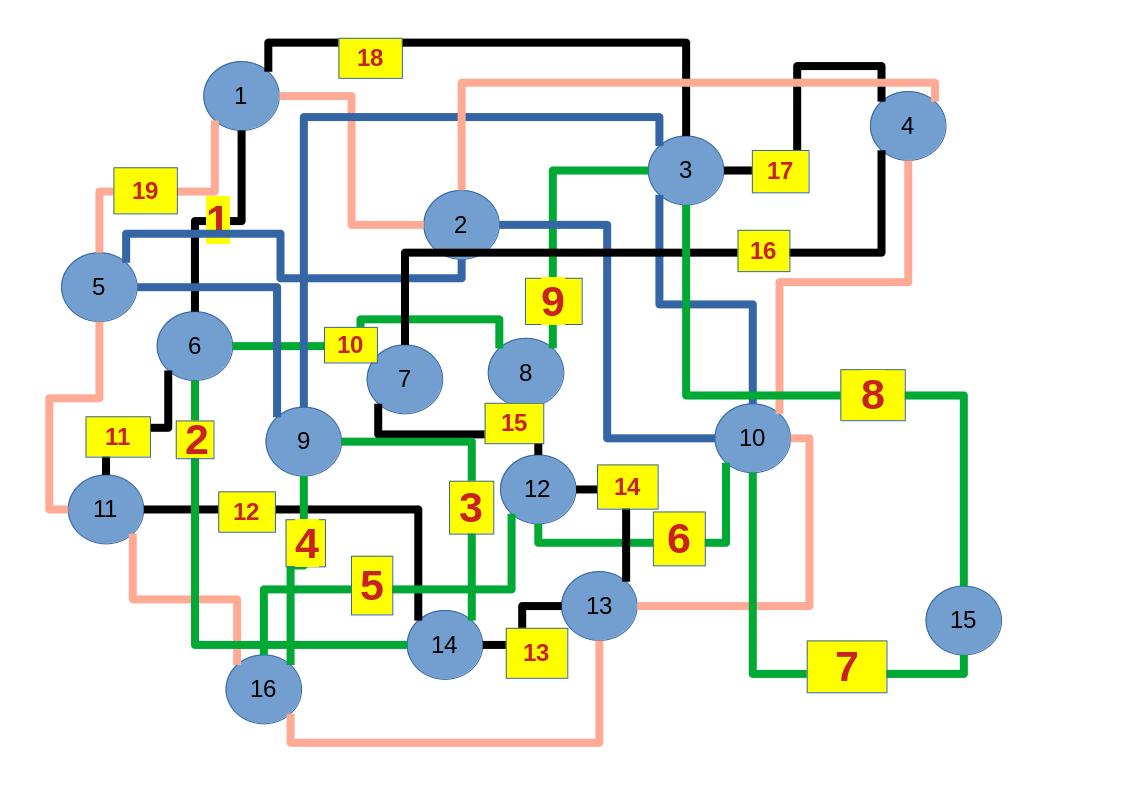
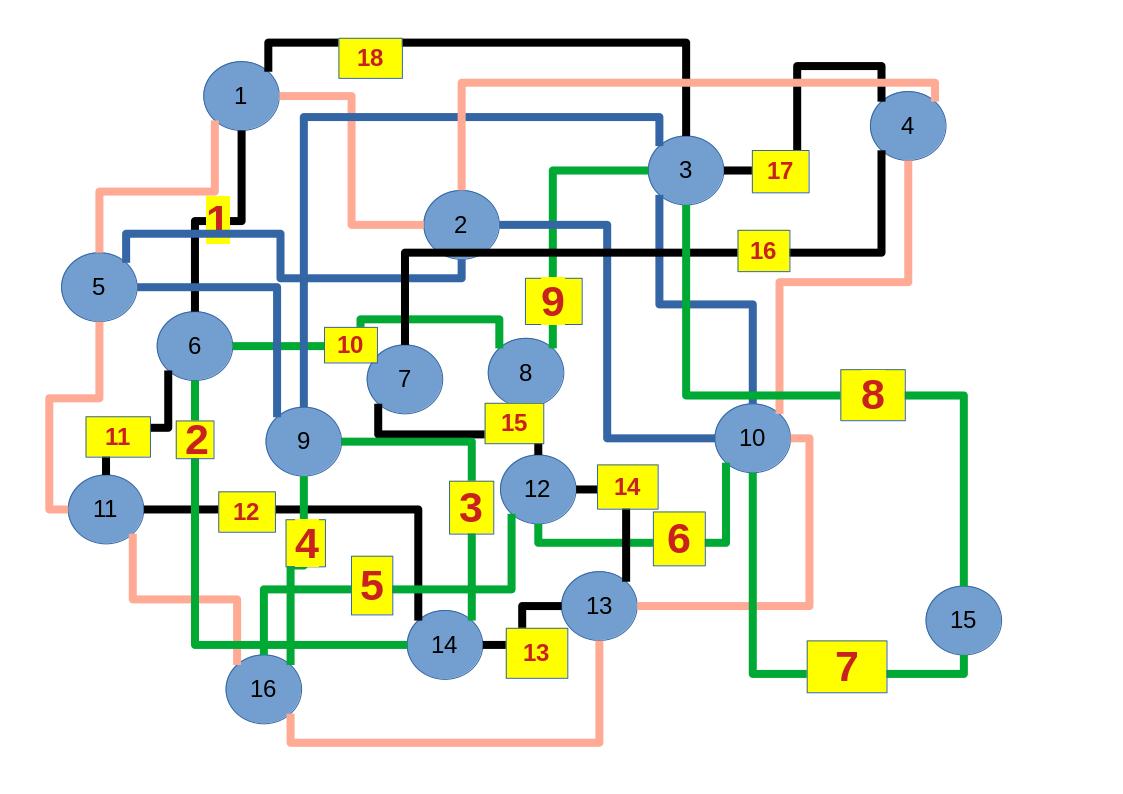
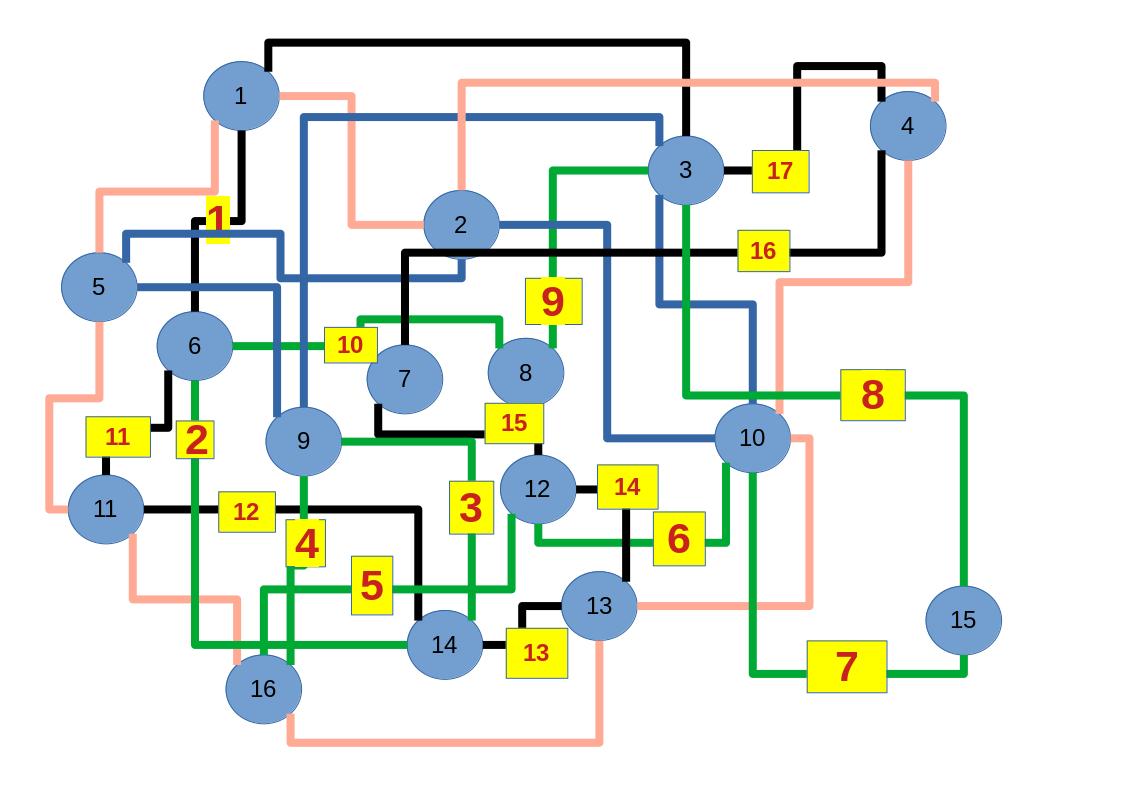
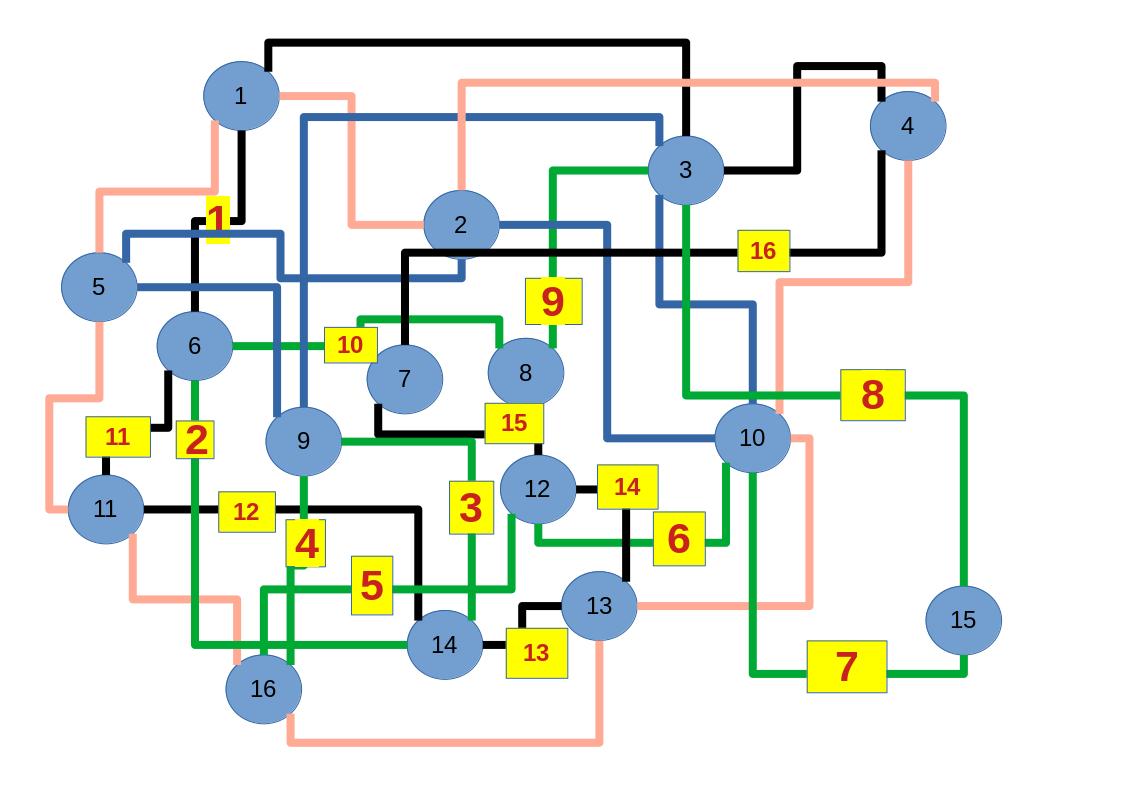
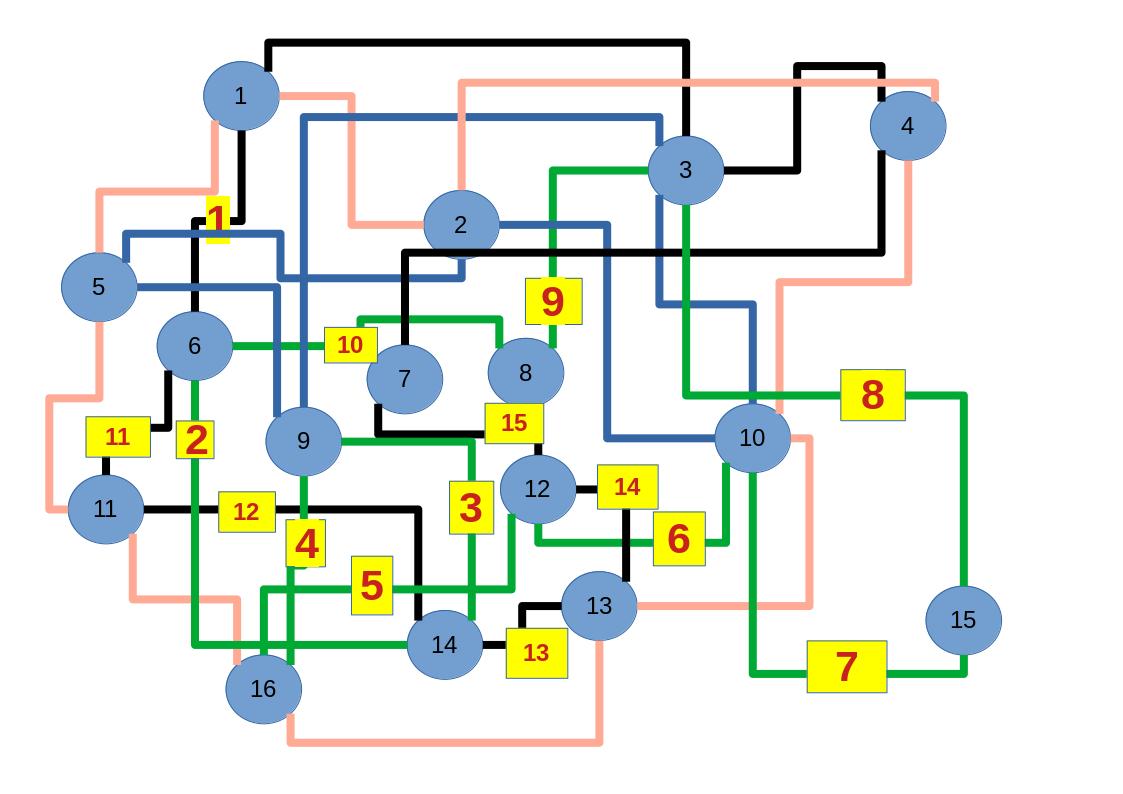
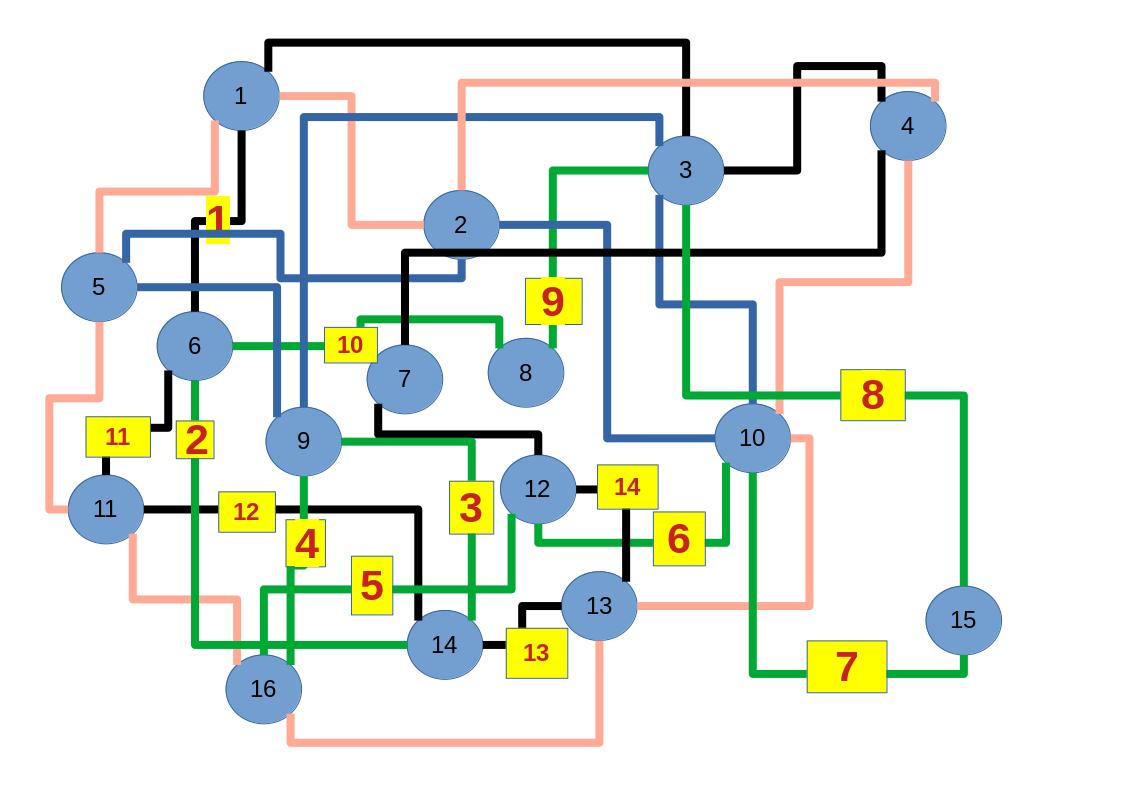
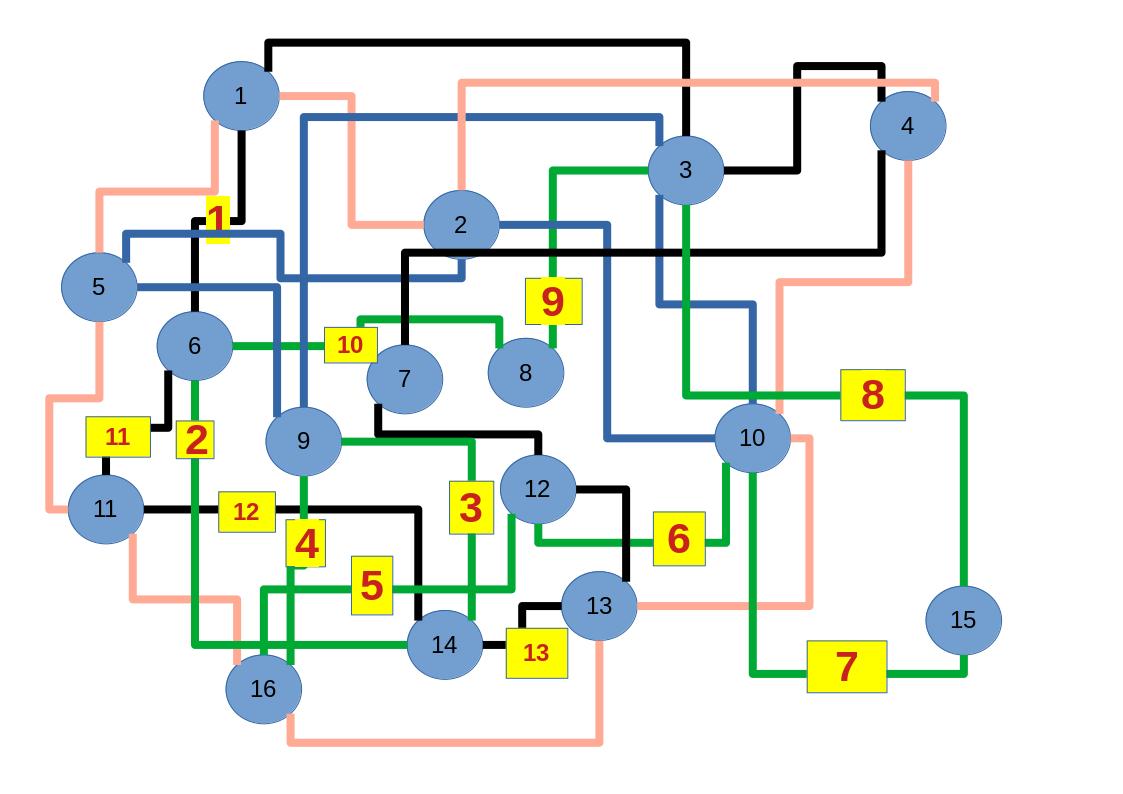
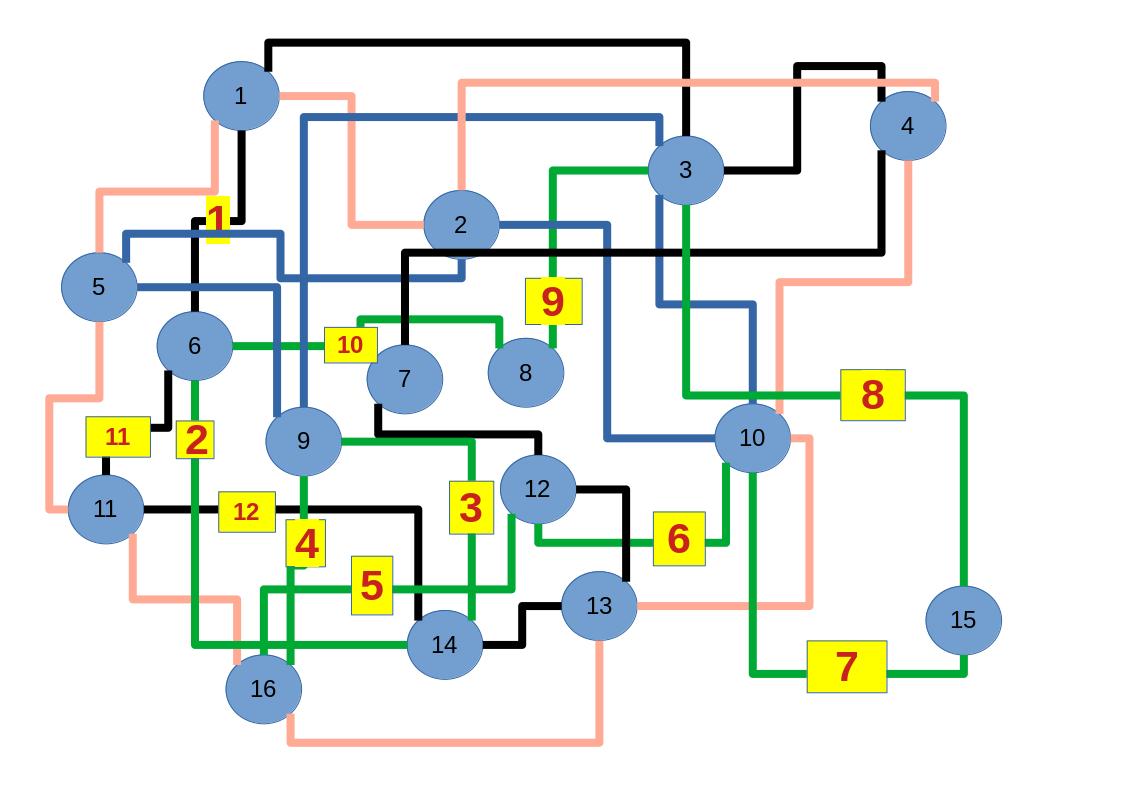
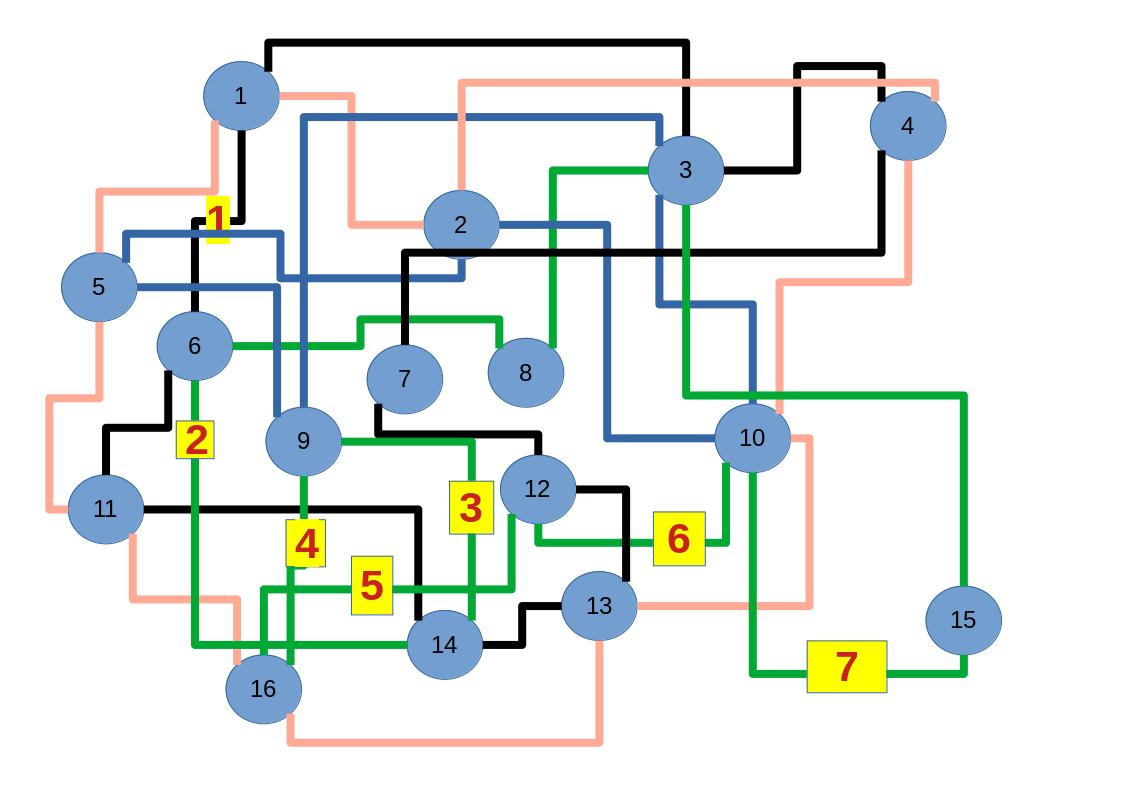
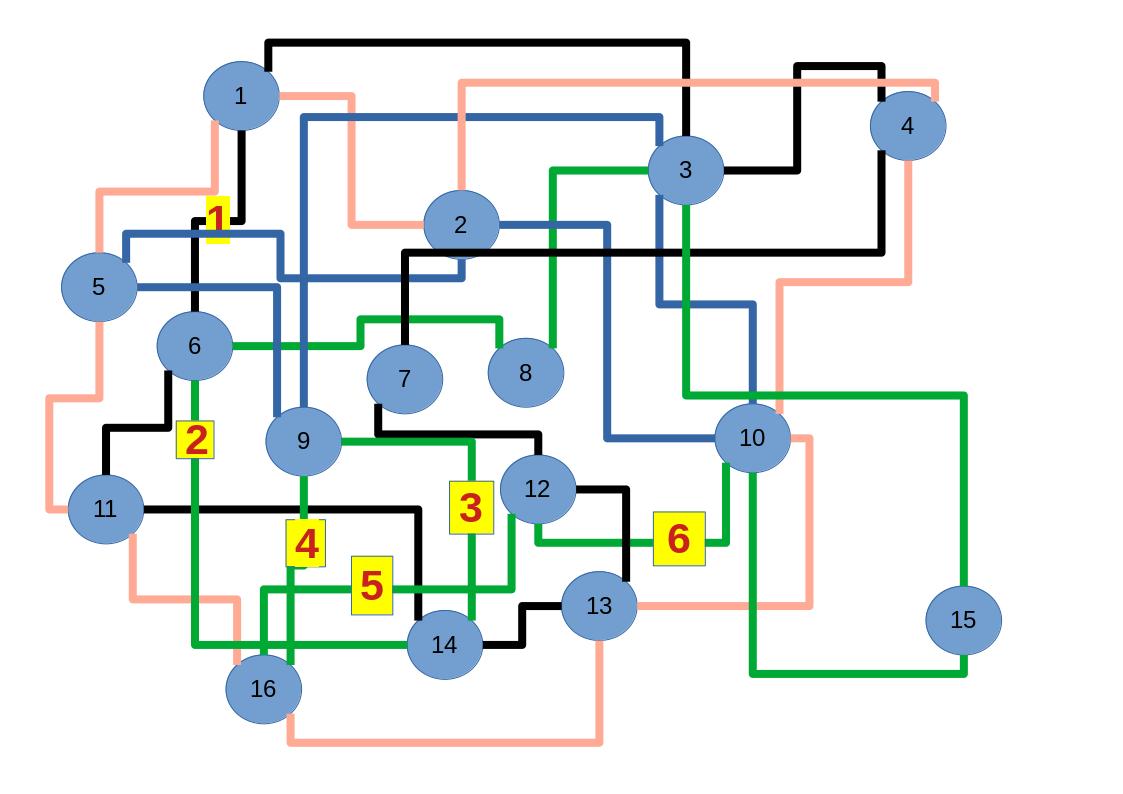
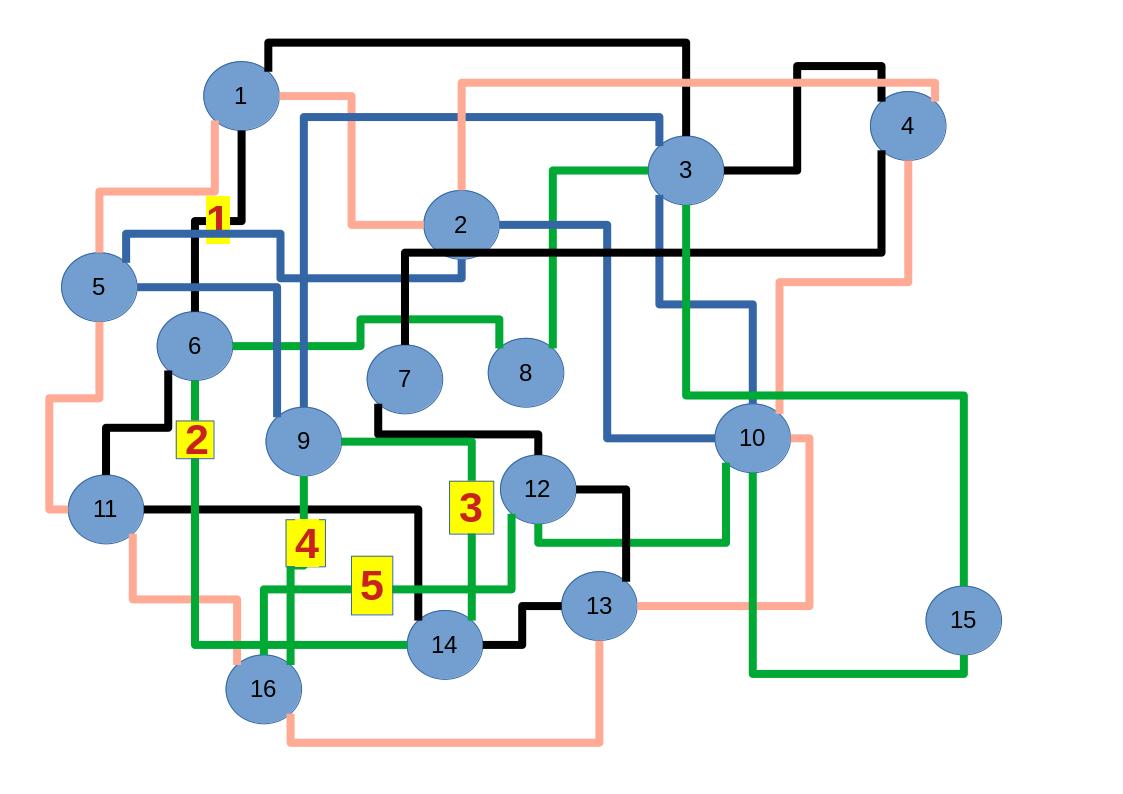
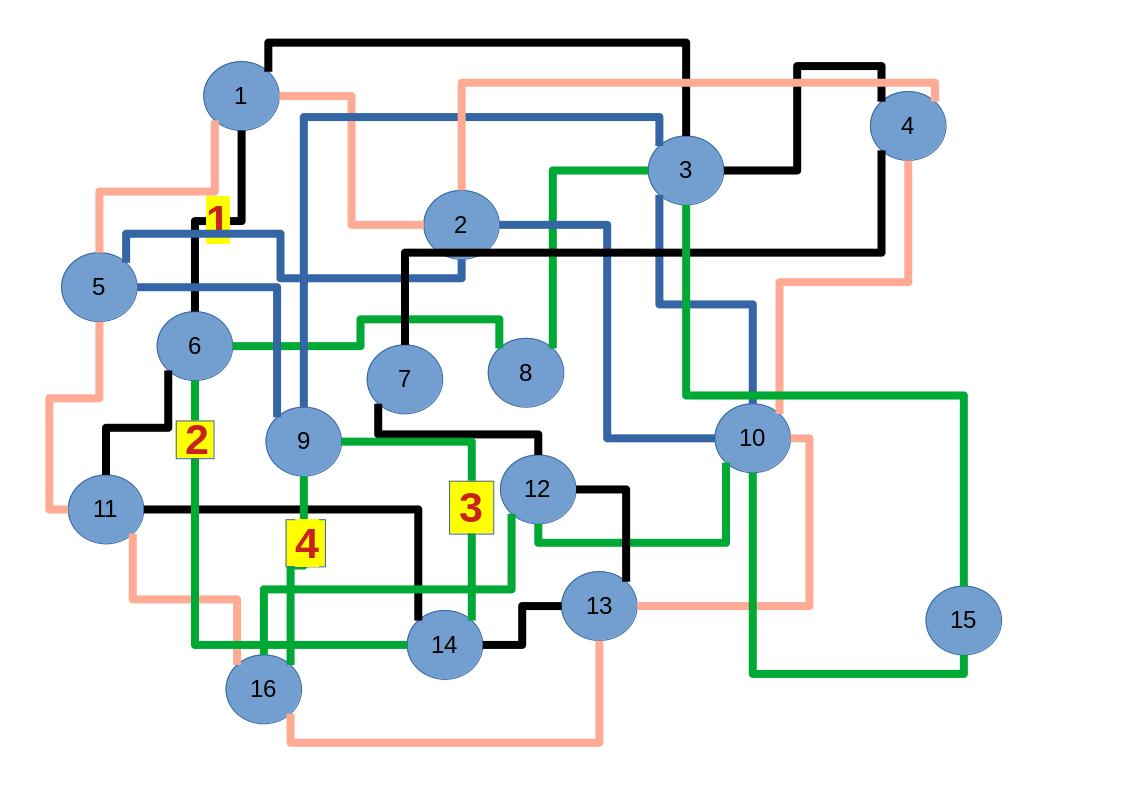
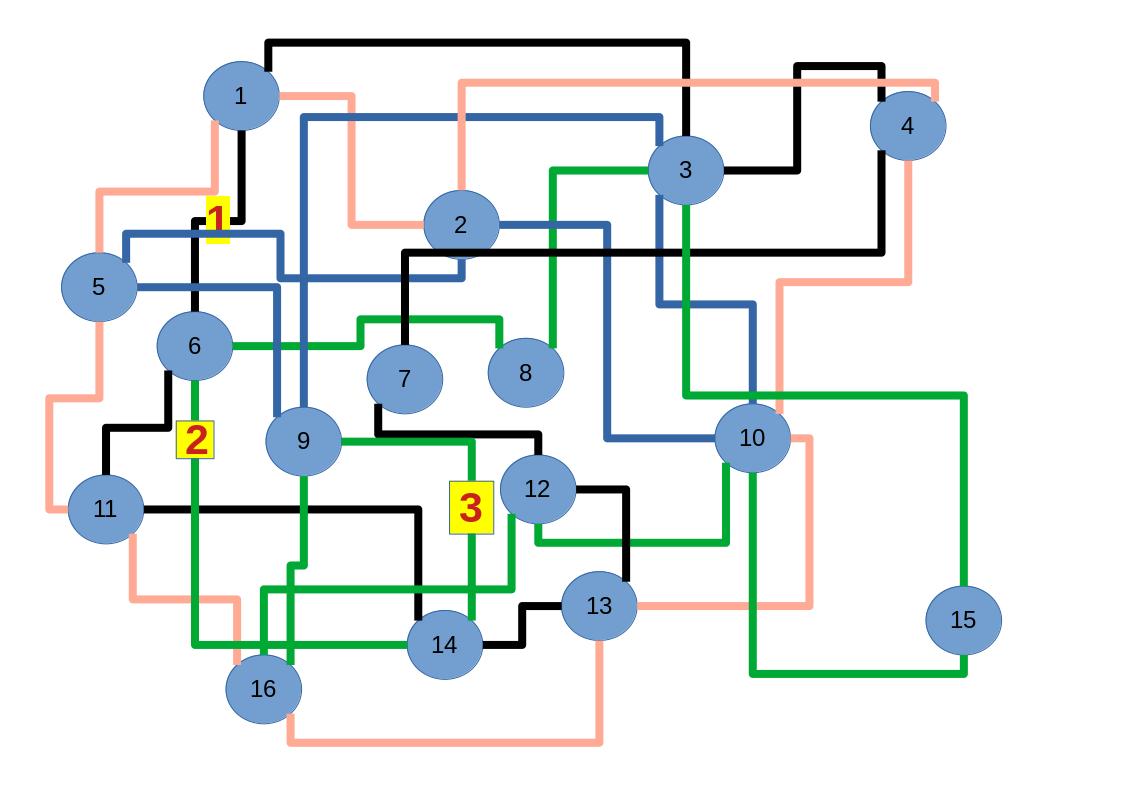
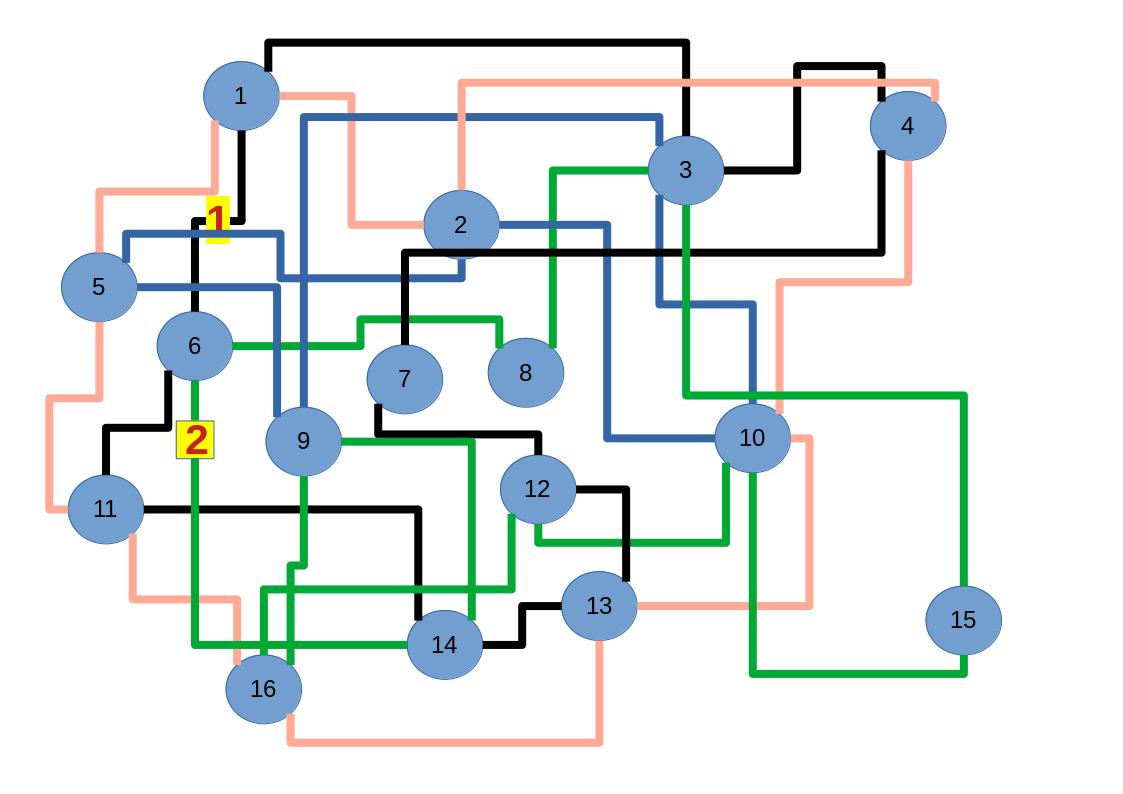
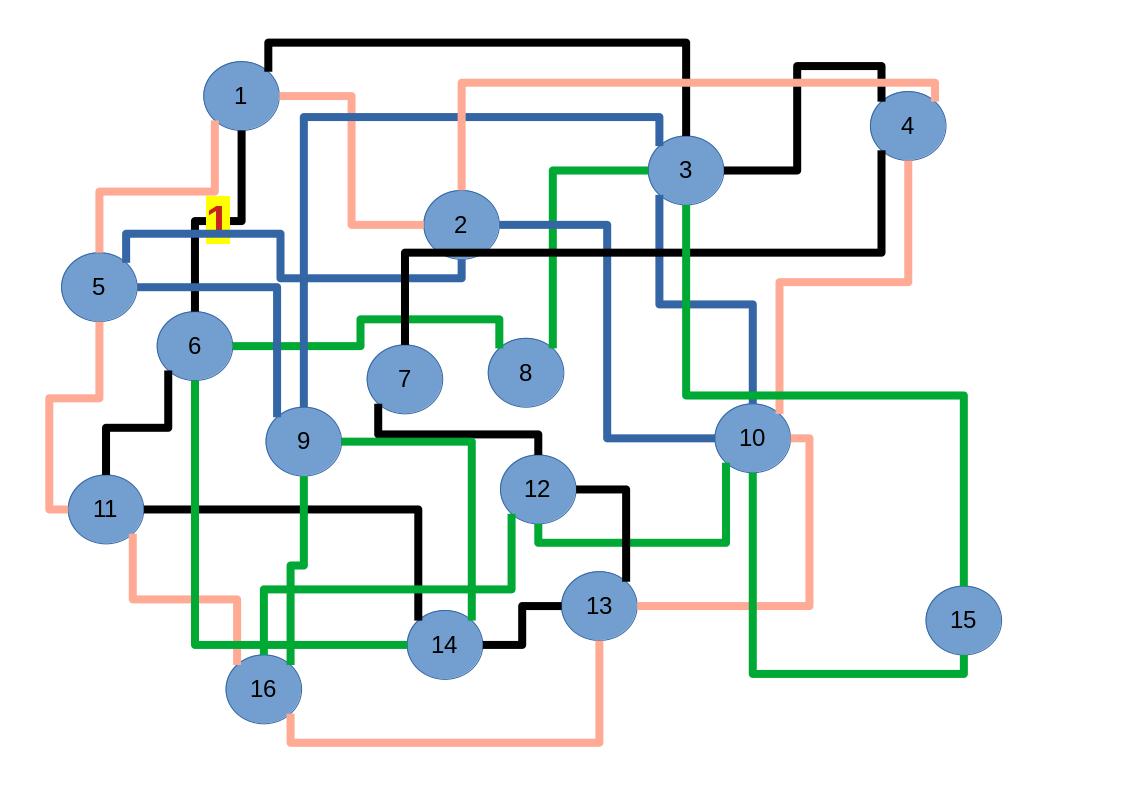
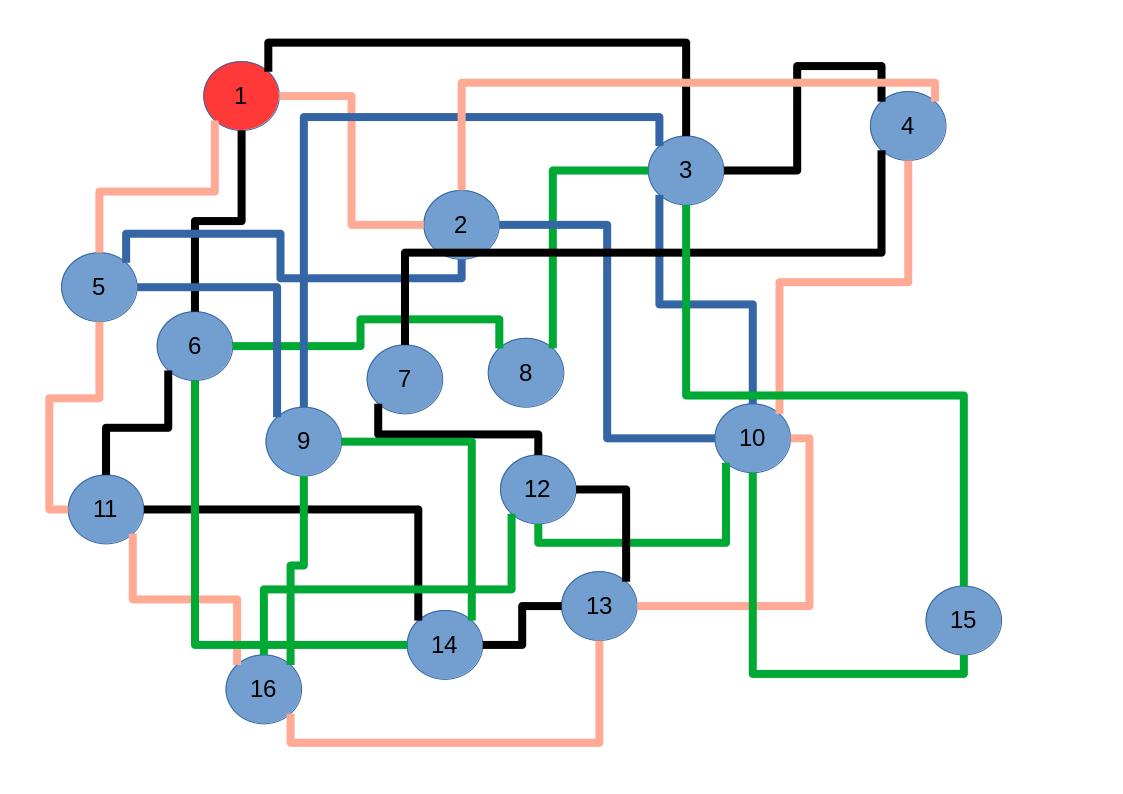
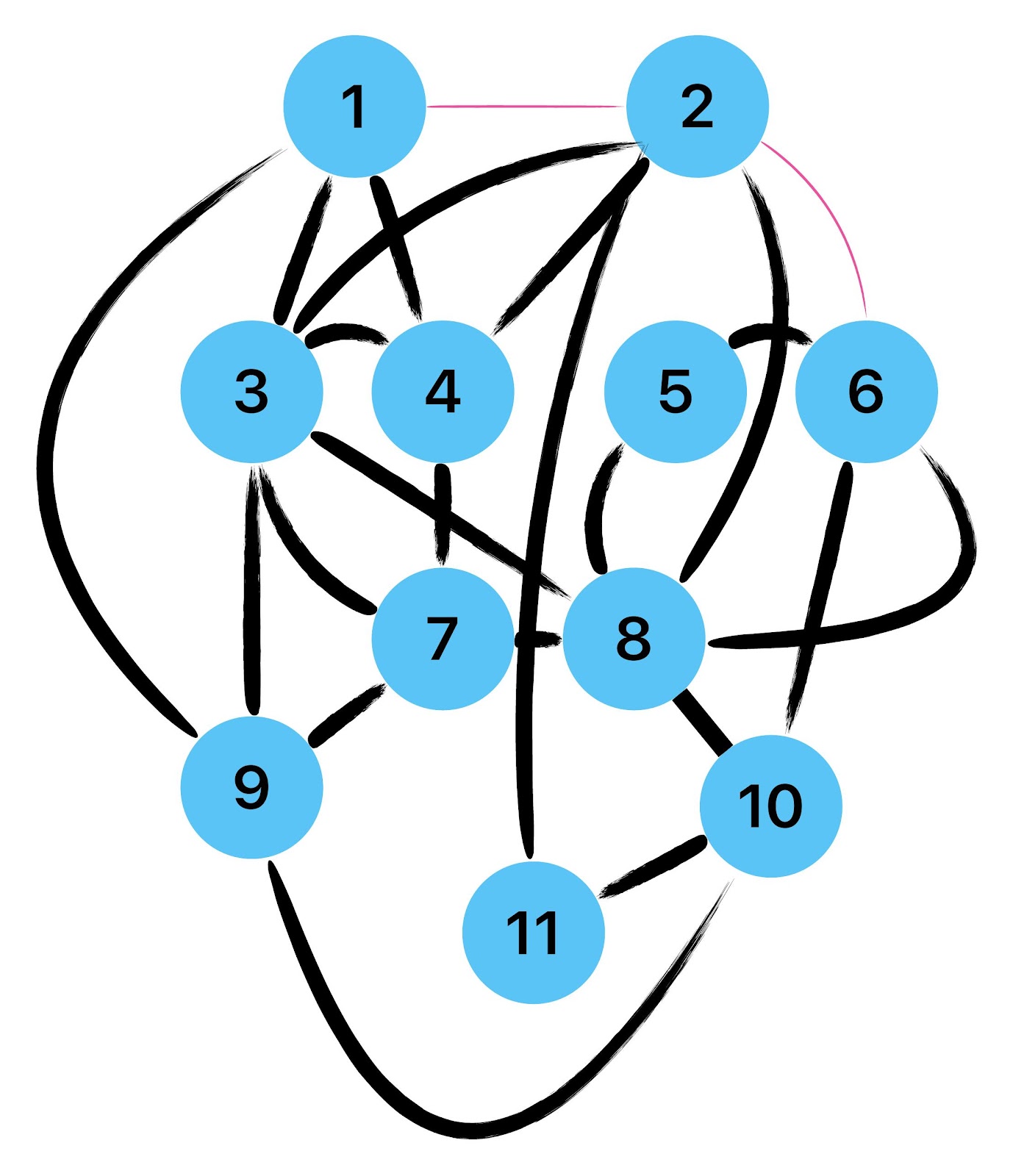
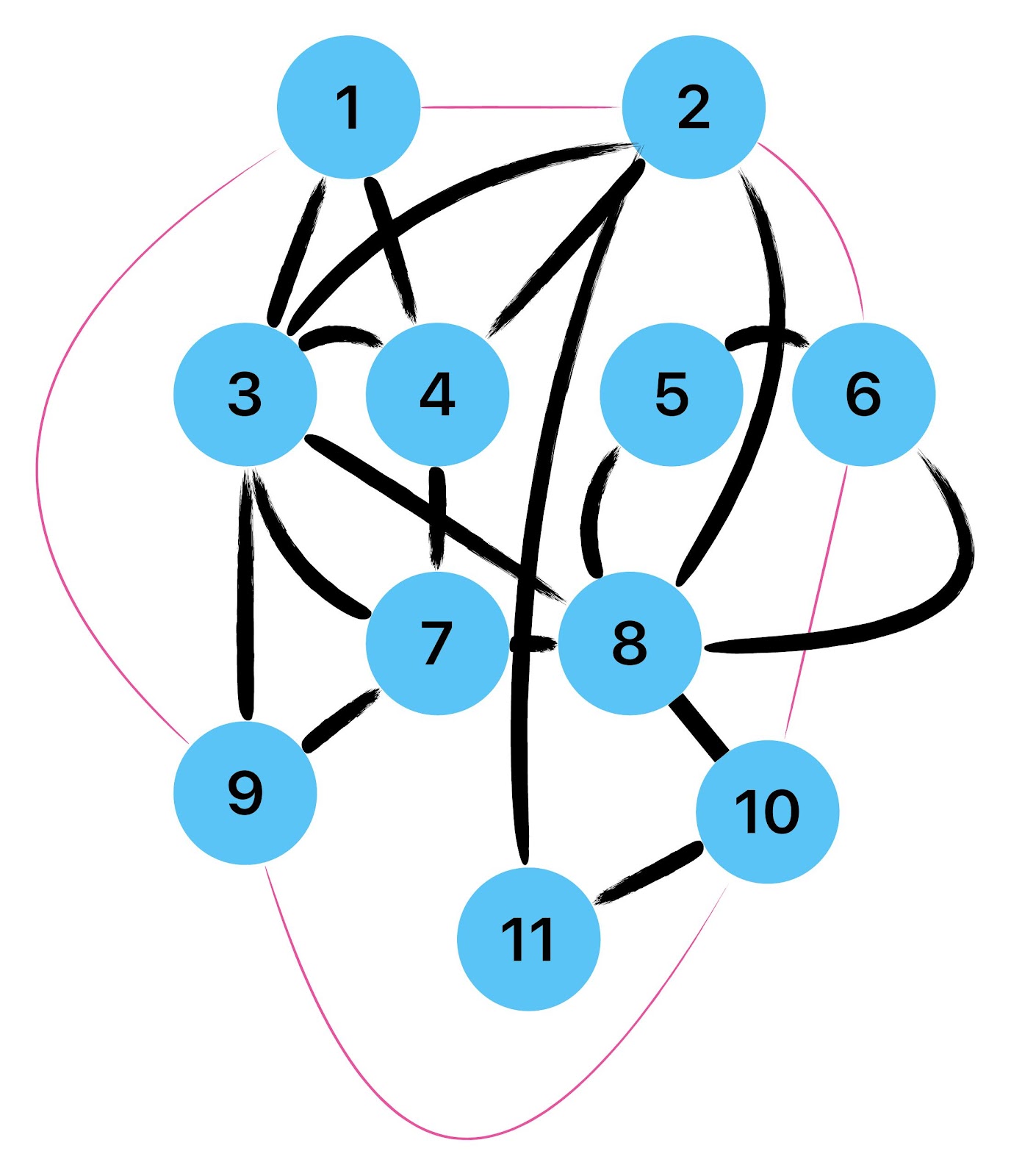
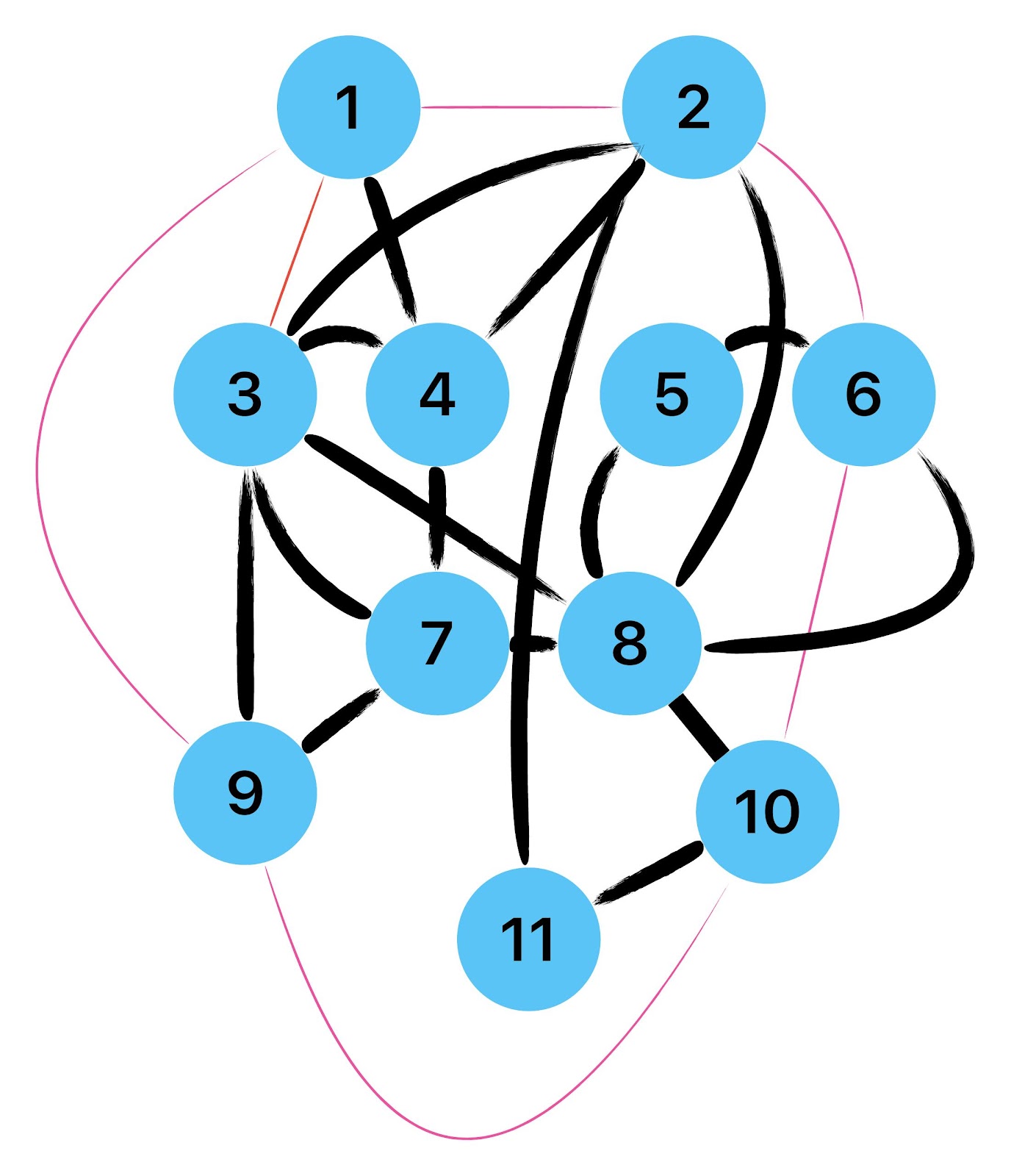
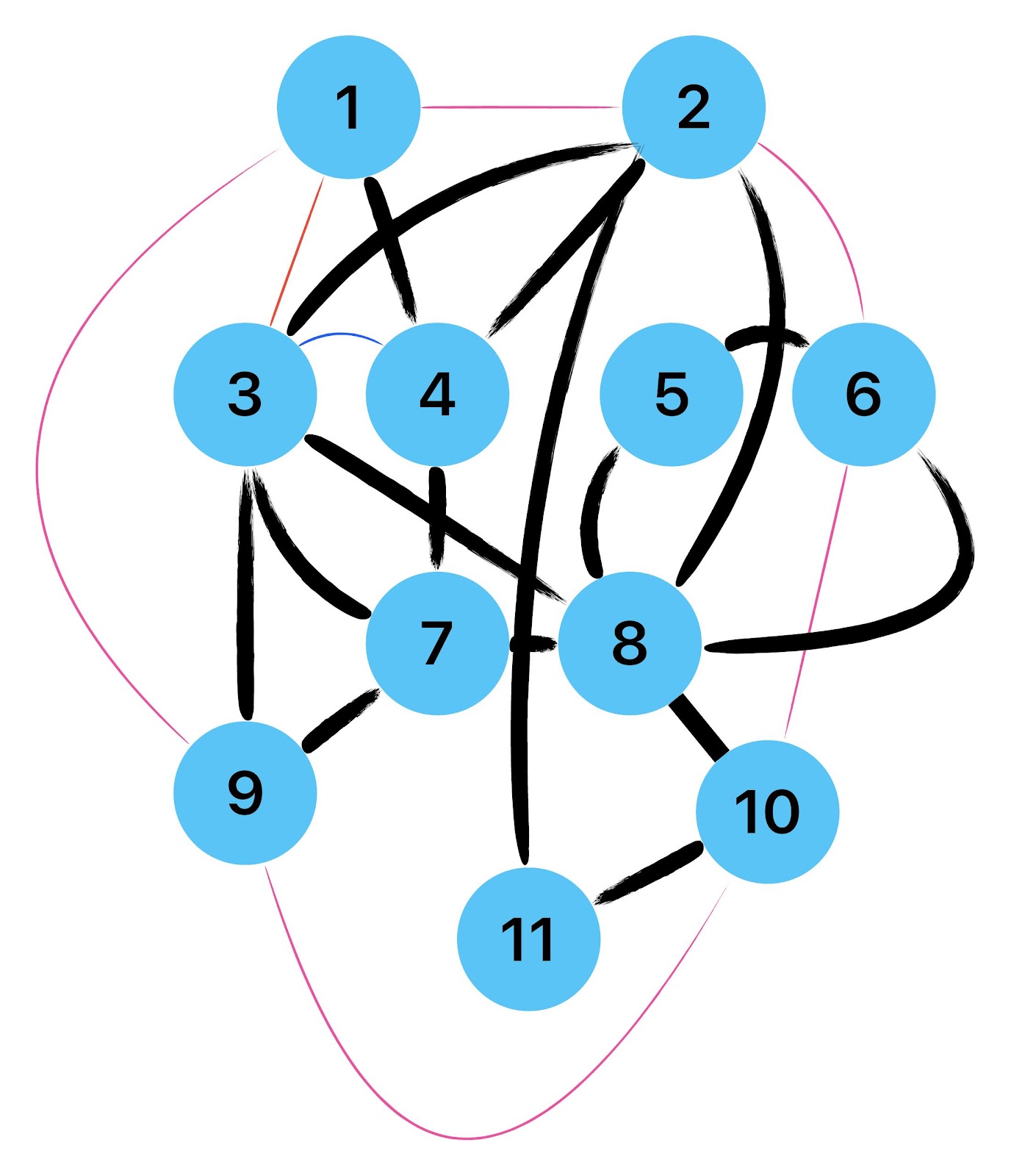
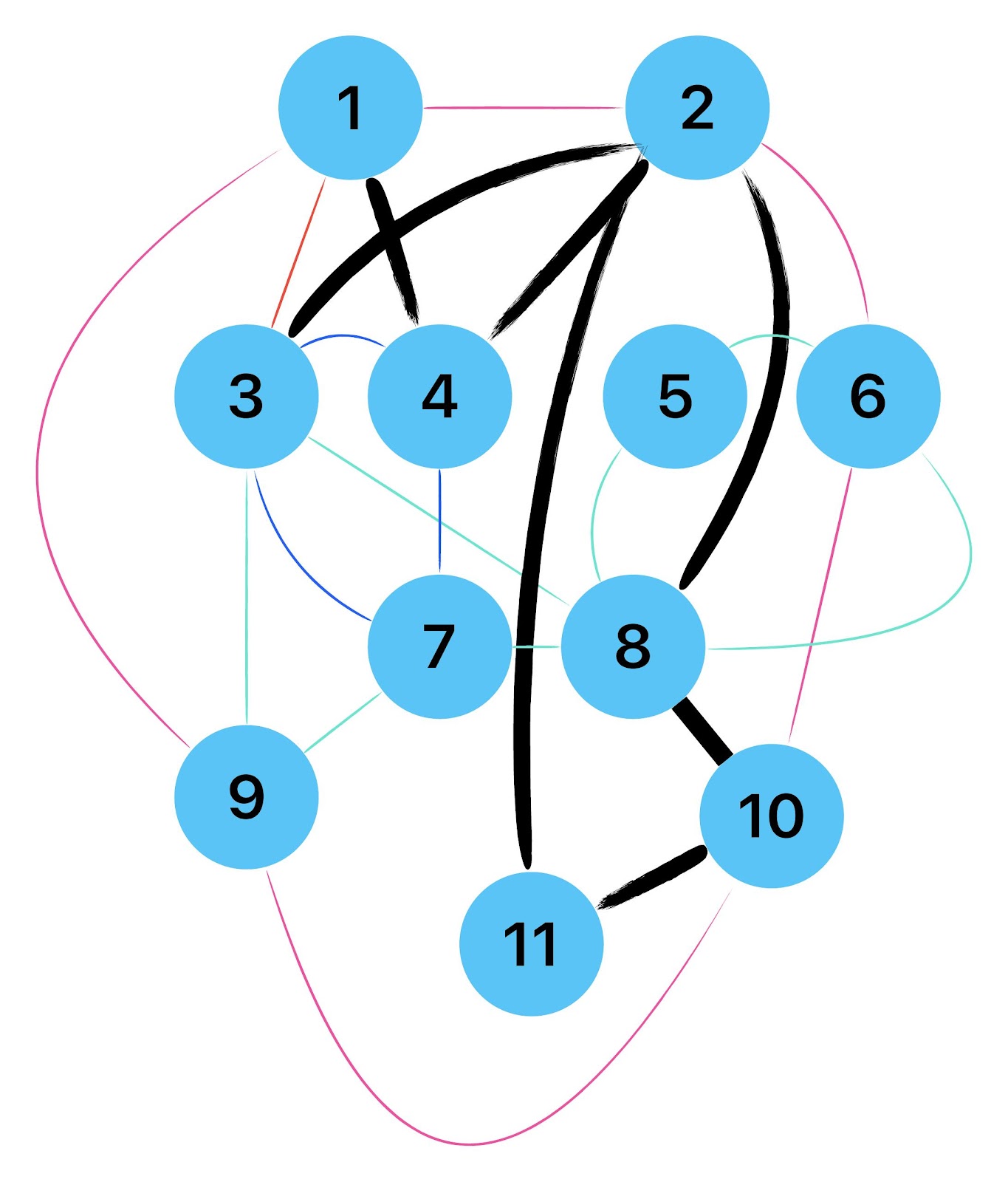
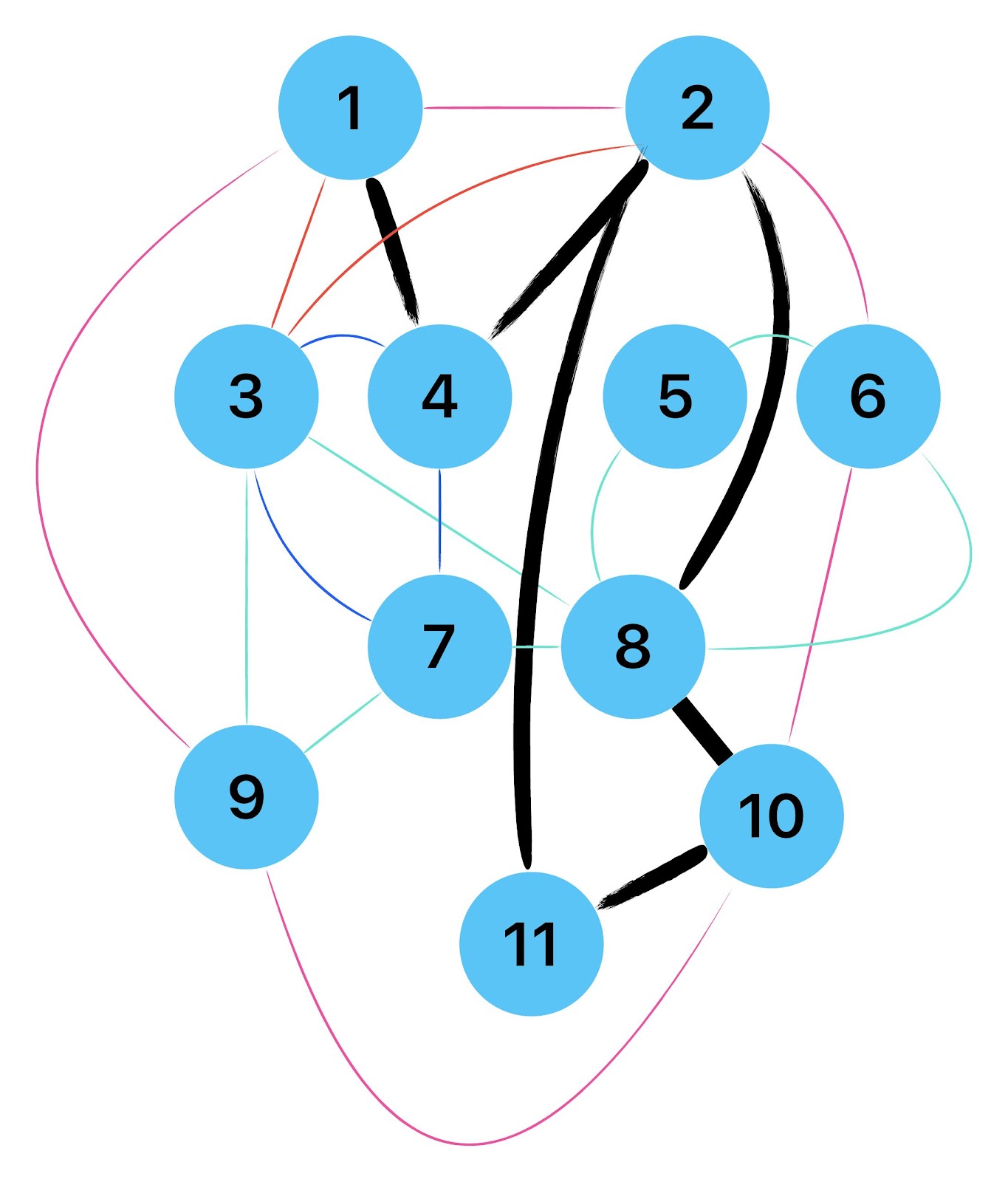
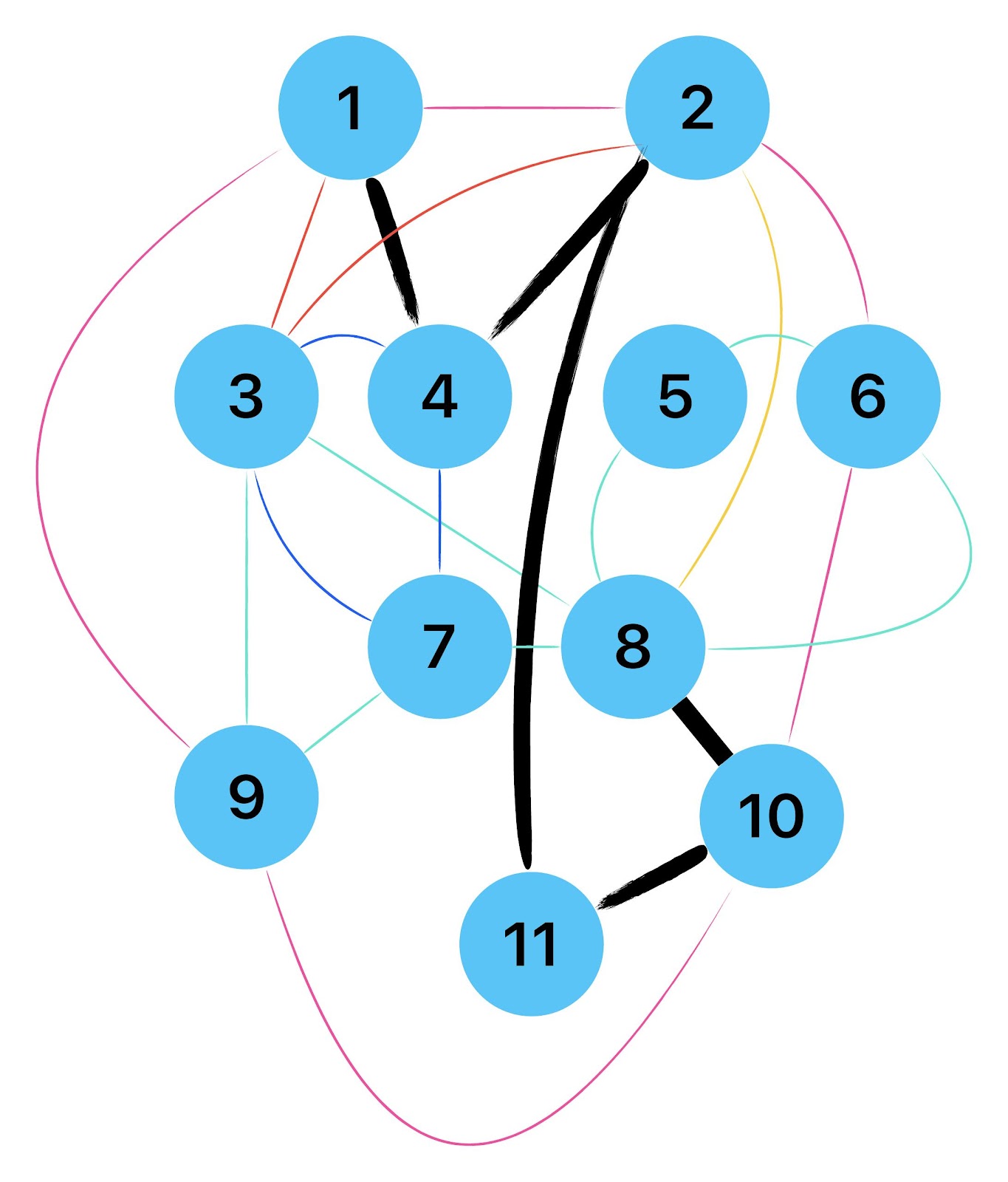
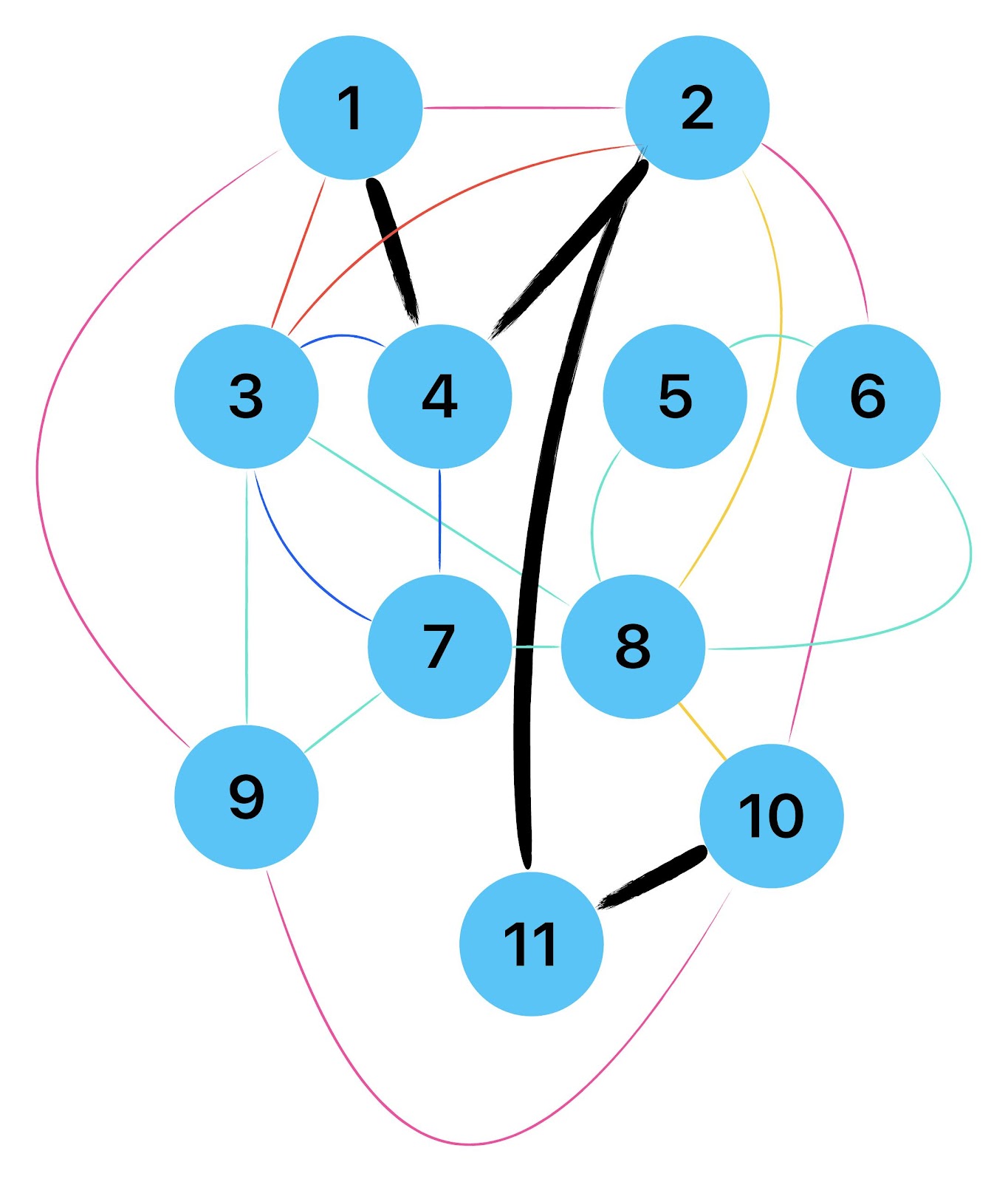
Zum lerntechnischen von diesem Skript. Ich denk was man da jetzt richtig machen kann es vor allem Folgendes das sind viele bestimmte Grafen drin. Ja und ich denke einerseits, dass das sicher zeigt beim Haus vom Nikolaus. Ich kann's jetzt mit ein Haus zeichnen und die Fernuni Hagen sagt, dass man beweisen kann, dass man's mit zwei Haeusern nicht zeichnen kann und in dem Skript in diesem Skript wird es wohl bestaetigt aber mit irgendeiner bestimmten Anzahl von Haeusern kann man's zeichnen und ich denke, dass sich das einfach lohnt, dass man ich hab das beim einfachen jetzt gelernt immer wieder zeichnet und dann bleibt es auch im Kopf sitzen und jetzt sind hier spezielle Grafen drin. Ich weiss nicht wie die heissen. Ich sag jetzt lieber keinen falschen Namen und das lohnt sich einfach immer die zu zeichnen genauso wie sich die Euler Tour wohl immer zu zeichnen lohnt, ich denke man sieht ganz klar, wenn man die Namen schoen auswendig lernt. Ich mach mal ne Liste von Namen was die Grafentheorie betrifft, was ich jetzt bisher weiss. Douglas und Amitabha Trip Party. Das wuerde jetzt falsch schreiben und so weiter was da sind jetzt laut und auch wieder neuen Namen das einfach mal die ganzen Namen lernt und so weiter das lohnt sich auf jeden Fall und denkt diese Grafen eben immer zeigen und was ich denke was das Wichtigste ueberhaupt ist und teilweise glaube ich das Wichtigste Mathematik Matrix Multiplikation wenn man das also ich sag mal das ist jetzt nichts besonderes, aber ich glaub man muss Matrizen Multiplikation so ueben dass er halt 100-prozentig sitzt das ist halt glaube ich der Unterschied. Natuerlich kann man das schon immer machen und verstanden haben aber ich glaub Matrizen Multiplikation, das muss automatisch gehen. Ich denke die sind so lernt technisch die Grundvoraussetzungen, mit dem man sich jetzt da dran wagen wird.
1.) Rechne die Zahl in binaer Darstellung in eine Dezimale Darstellung um
1010111011010000b 44752d
2.) Rechne die Zahl in dezimal darstellung in eine Binaerdarstellung um
31410 0111101010110010
3.) Addiere die drei Zahlen schriftlich
43879
+ 38291
+ 52731
-----------------
134901
4.) Subtrahiere die letzten drei Zahlen schriftlich von der ersten schriftlich
53880
- 7593
- 11901
- 13406
-----------------
20980
5.) Rechne die Zahl ins zweier komplement um, mit 8 Bit - und subtrahiere diese zahl von der ersten und rechne das Ergebnis nach dezimal
105 -88 = 17
01101001 10101000 = 00010001
6.) Multipliziere die zwei Zahlen schriftlich
17838*12052 = 214983576
7.) Dividiere die zwei Zahlen schriftlich
640/13610 = 0
8.) Errechne x Logarithmisch mit dem Taschenrechner
36316\^x = 1259078189
9.) Errechne mit dem Abakus
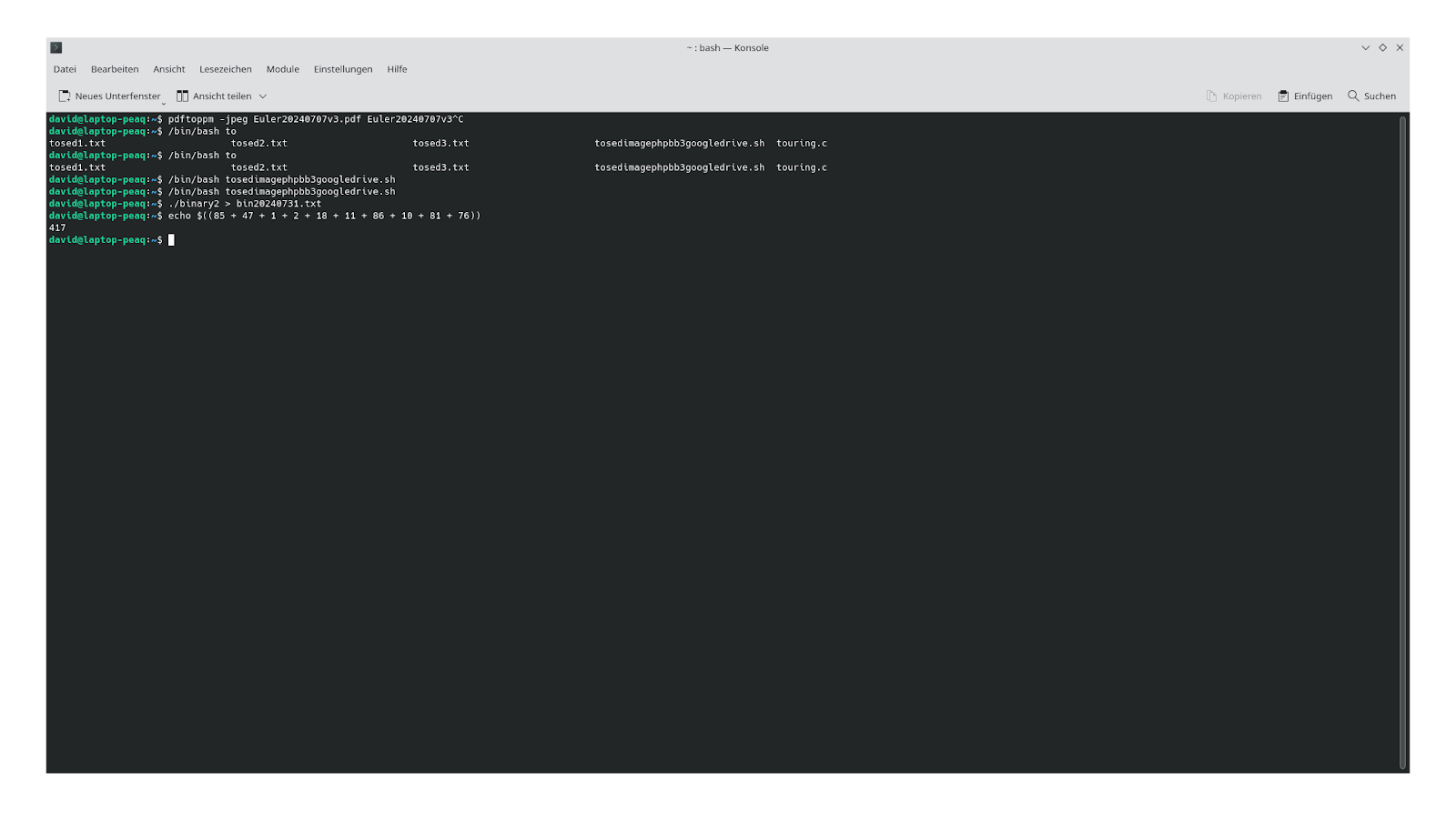
85 + 47 + 1 + 2 + 18 + 11 + 86 + 10 + 81 + 76
david@laptop-peaq:~\$ echo \$((85 + 47 + 1 + 2 + 18 + 11 + 86 + 10 + 81 + 76)) 417 david@laptop-peaq:~\$











1.) Rechne die Zahl in binaer Darstellung in eine Dezimale Darstellung um
1010111011010000b 44752d
2.) Rechne die Zahl in dezimal darstellung in eine Binaerdarstellung um
31410 0111101010110010
3.) Addiere die drei Zahlen schriftlich
43879
+ 38291
+ 52731
-----------------
134901
4.) Subtrahiere die letzten drei Zahlen schriftlich von der ersten schriftlich
53880
- 7593
- 11901
- 13406
-----------------
20980
5.) Rechne die Zahl ins zweier komplement um, mit 8 Bit - und subtrahiere diese zahl von der ersten und rechne das Ergebnis nach dezimal
105 -88 = 17
01101001 10101000 = 00010001
6.) Multipliziere die zwei Zahlen schriftlich
17838*12052 = 214983576
7.) Dividiere die zwei Zahlen schriftlich
640/13610 = 0
8.) Errechne x Logarithmisch mit dem Taschenrechner
36316\^x = 1259078189
9.) Errechne mit dem Abakus
85 + 47 + 1 + 2 + 18 + 11 + 86 + 10 + 81 + 76
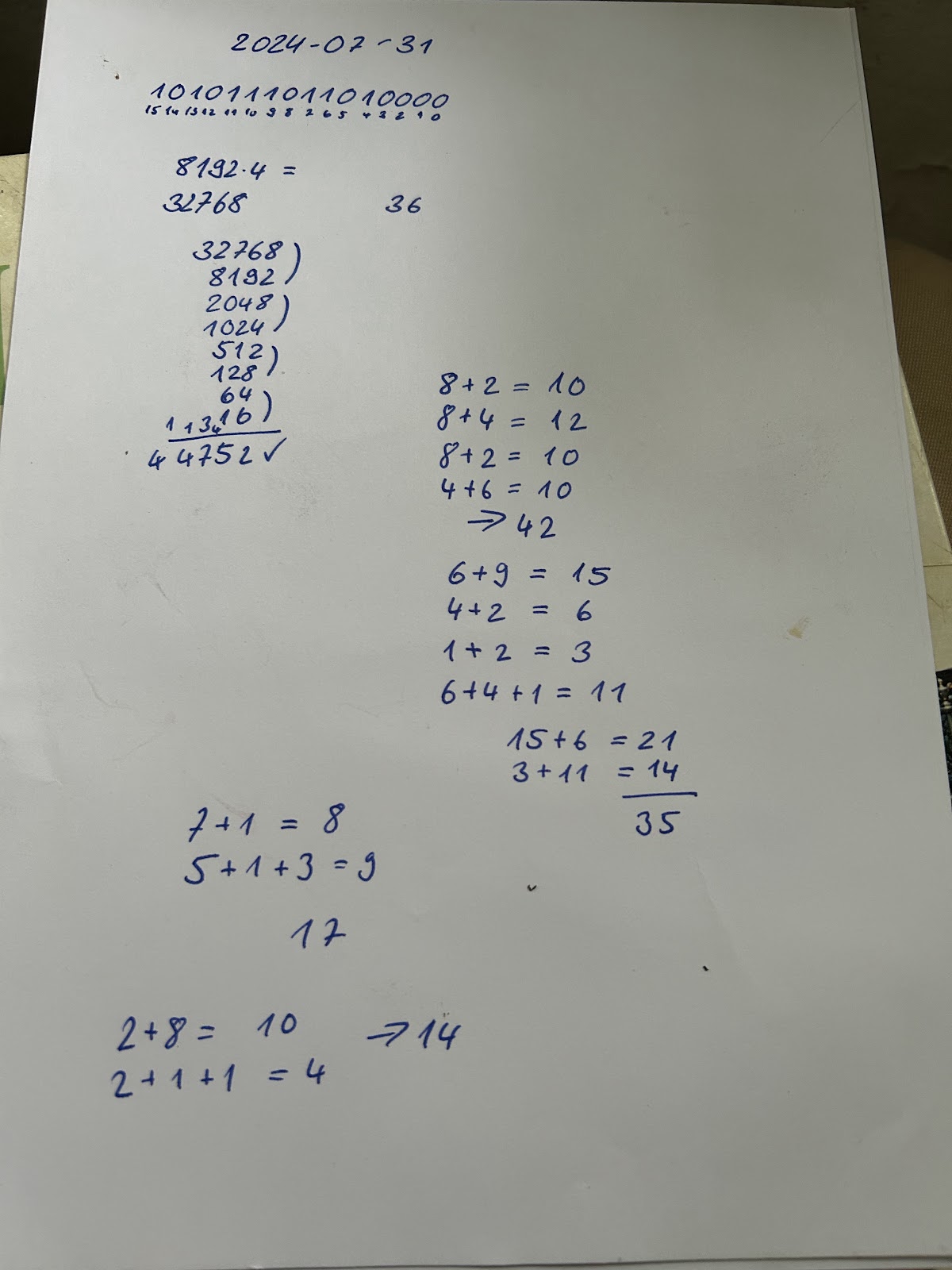


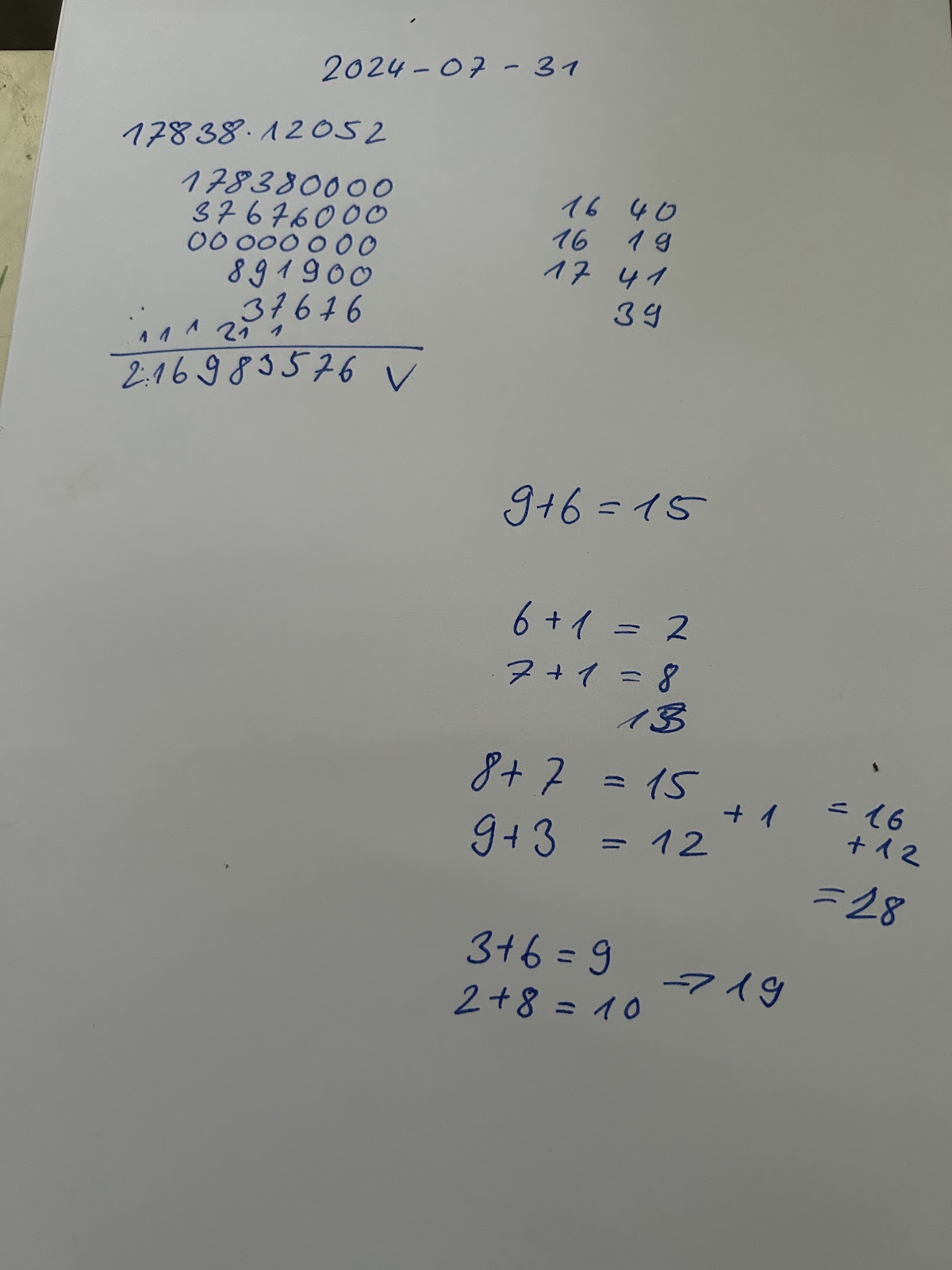
david@laptop-peaq:~\$ echo \$((212*64+42)) 13610 david@laptop-peaq:~\$ /bin/bash tosedimagephpbb3googledr
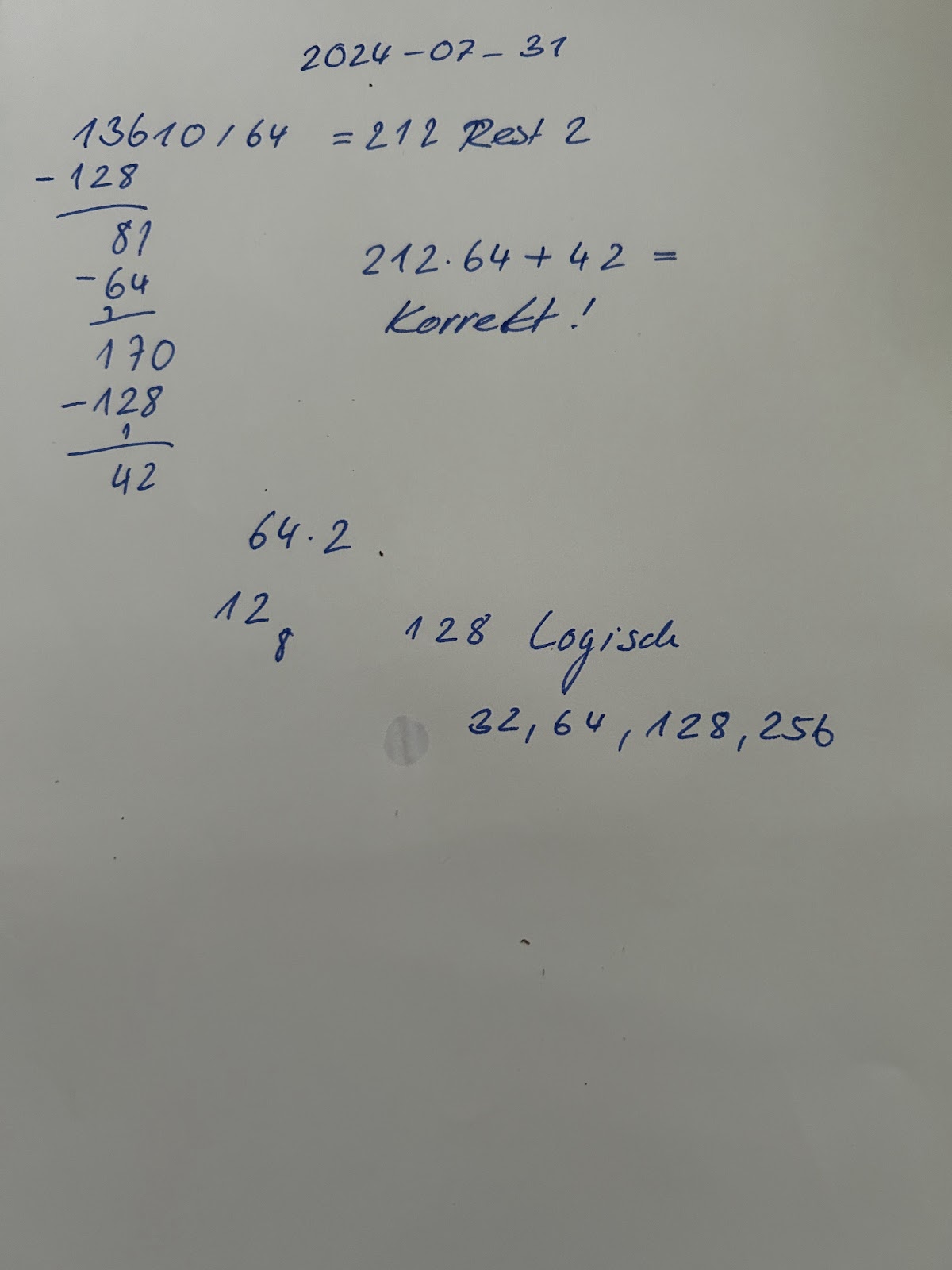

Da ist grad irgendwo fuer mich nicht korrigierbar Fehler drin im Moment nicht korrigierbar aber ich hab jetzt keine Lust
Ich mein, ich hatte auch aus Versehen zweimal die Nummer sechs verwendet verschiedene Knoten

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define NO_ELEM -1
#define MAX_LINE_COLUMN 4
#define MIN_LINE_COLUMN 4
#define MAX_VAL 10
#define MIN_VAL 0
int main (void) {
time_t t;
int m, n, s, q;
int i, j;
int g, h;
int a [MAX_LINE_COLUMN + MIN_LINE_COLUMN][MAX_LINE_COLUMN + MIN_LINE_COLUMN];
int b [MAX_LINE_COLUMN + MIN_LINE_COLUMN][MAX_LINE_COLUMN + MIN_LINE_COLUMN];
int ab [MAX_LINE_COLUMN + MIN_LINE_COLUMN][MAX_LINE_COLUMN + MIN_LINE_COLUMN];
for (i = 0; i < MAX_LINE_COLUMN; i++)
for (j = 0; j < MAX_LINE_COLUMN; j++) {
a [i] [j] = NO_ELEM;
b [i] [j] = NO_ELEM;
}
srand ((unsigned) time (\&t));
m = (rand () % MAX_LINE_COLUMN) + MIN_LINE_COLUMN;
n = (rand () % MAX_LINE_COLUMN) + MIN_LINE_COLUMN;
s = (rand () % MAX_LINE_COLUMN) + MIN_LINE_COLUMN;
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
a [i] [j] = (rand () % MAX_VAL) + MIN_VAL;
}
}
for (i = 0; i < n; i++) {
for (j = 0; j < s; j++) {
b [i] [j] = (rand () % MAX_VAL) + MIN_VAL;
}
}
for (g = 0; g < m; g++) {
for (h = 0; h < s; h++) {
ab [g][h] = 0;
for (j = 0; j < n; j++)
ab [g][h] += a [g][j] * b [j][h];
}
}
if (m >= n)
q = m;
else
q = n;
printf ("\documentclass[a4paper]{article}n");
printf ("\usepackage{german,amsmath,amsfonts}n");
printf ("\begin{document}n");
printf ("\$\$m = %i,n = %i,s = %i\$\$", m, n, s);
printf ("\$\$\left(\begin{array}{");
for (j = 0; j <= n; j++) printf ("c");
printf ("}");
for (i = 0; i < q; i++) {
if (i < m) {
for (j = 0; j < n; j++) {
printf ("%i\&", a [i][j]);
}
printf ("n");
}
}
printf ("\end{array}\right)");
printf ("\left(\begin{array}{");
for (j = 0; j <= s; j++) printf ("c");
printf ("}");
for (i = 0; i < q; i++) {
if (i < n) {
for (j = 0; j < s; j++) {
printf ("%i\&", b [i][j]);
}
printf ("n");
}
printf ("n");
}
printf ("\end{array}\right)n");
printf ("= \left(\begin{array}{");
for (j = 0; j <= s; j++) printf ("c");
printf ("}");
for (i = 0; i < m; i++) {
for (j = 0; j < s; j++)
printf ("%i\&", ab [i][j]);
printf ("n");
}
printf ("n");
printf ("\end{array}\right)\$\$n");
printf ("\end{document}n");
return 0;
}