Nächste Seite: Die Eulertour in Python Aufwärts: Graphen, Schaltwerke und Zahlen Vorherige Seite: Re: Das neue Auswendig
1.) Rechne die Zahl in binaer Darstellung in eine Dezimale Darstellung um
1001111110010101b 40853d
2.) Rechne die Zahl in dezimal darstellung in eine Binaerdarstellung um
16469 0100000001010101
3.) Addiere die drei Zahlen schriftlich
23541
+ 23334
+ 14343
-----------------
61218
4.) Subtrahiere die letzten drei Zahlen schriftlich von der ersten schriftlich
39570
- 9348
- 12752
- 1425
-----------------
16045
5.) Rechne die Zahl ins zweier komplement um, mit 8 Bit - und subtrahiere diese zahl von der ersten und rechne das Ergebnis nach dezimal
60 -16 = 44
00111100 11110000 = 00101100
6.) Multipliziere die zwei Zahlen schriftlich
11627*51089 = 594011803
7.) Dividiere die zwei Zahlen schriftlich
43989/25345 = 1
8.) Errechne x Logarithmisch mit dem Taschenrechner
18692\^x = 1704893420
9.) Errechne mit dem Abakus
56 + 95 + 72 + 84 + 77 + 5 + 48 + 47 + 58 + 55
Als erstes kommt die Rechnung mit dem Abakus. Ab morgen oder uebermorgen habe ich einen zweiten, dann kann ich auch laengere Zahlen multiplizieren. Ich hatte ja ein Bash Skript geschrieben, das die Zahlen einzeln addiert, falls inzwischen ein Fehler auftaucht.
#!/bin/bash
a=(\$1)
i=0
z=0
while [ \$i -lt 19 ]
do
echo "Plus \${a[\$i]}"
z=\$((\$z+\${a[\$i]}))
i=\$((\$i+2))
echo \$z
done
echo \$((\$1))
david@laptop-peaq:~/progs2_20240801\$ /bin/bash add3.sh "56 + 95 + 72 + 84 + 77 + 5 + 48 + 47 + 58 + 55" Plus 56 56 Plus 95 151 Plus 72 223 Plus 84 307 Plus 77 384 Plus 5 389 Plus 48 437 Plus 47 484 Plus 58 542 Plus 55 597 597 david@laptop-peaq:~/progs2_20240801\$












So im naechsten Schritt schreibe ich ein kleines Programm, um die Maja Vigesimalziffern zu ueben, dann uebe ich kurrent Schrift.
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main (void) {
time_t t;
int i;
srand ((unsigned )time (\&t));
for (i = 0; i < 10; i++)
printf ("%it", rand () % 20);
printf ("n");
return 0;
}
5 11 0 17 13 17 11 2 8 5
wikipedia:

Jetzt uebe ich kurrent Schrift

Jetzt mache ich zwei Rechenaufgaben dann spiele ich Poker

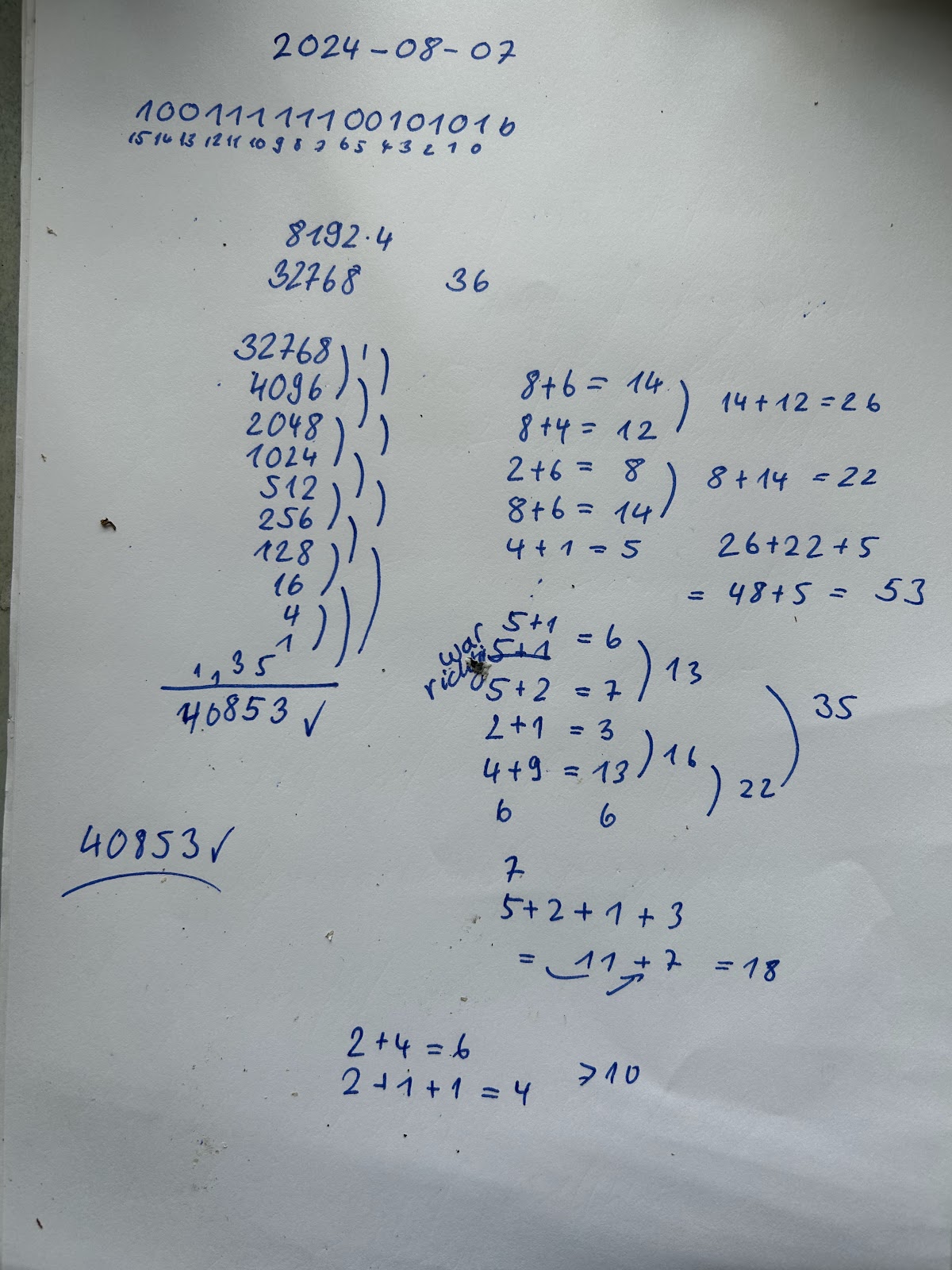
ich spiele jetzt poker. Vorher einen Kaffee und ein bisschen Pause









Im naechsten Schritt schreibe ich ein Programm, damit ich das Blatt beim Poker schneller vergleichen lerne, es ist generell klar, auswendig
Das ist generell klar, ebenso wie klar sein duerfte, dass Straight Flush, das staerkste ist. Somit ueber Full House liegt und es leuchtet auch noch ein dass dazwischen 4 of a kind liegt. Bei Blaze und Round the Corner Straight wird es schon anders. Ich kann mir die Namen merken, indem ich sie herunter bete, aber gerade beim Poker ist das keine gute Idee. Denn hier muss man ein Poker Face zeigen und niemand sollte einem dabei zuhoeren wie man es runter betet, denn niemand soll auch nur im mindesten erfahren was man hat
Natuerlich erkenne ich jedes Blatt auf einen Blick, deswegen uebe ich ja seit langem mit mir selber
Auch klappen vergleiche oft relativ gut, doch denken sie an die 12 Zahlen
{1,2,3,4,5,6,7,8,9,10,11,12}
Wuerden sie sich hier jemals vertun, koennten also nicht fuer jede Zahl einzeln ein Partialordnung
6 < 9
auf anhieb richtig beantworten. so moechte ich das bei Poker haben und bei den Tierkreiszeichen
also schreibe ich ein Programm. Es stellt die Relation zwischen zwei her. die 12 Namen speichere in einem Feld. Um es dann etwas komplizierter zu machen, kommt ein zweiter Teil ins Programm, was die Groessenrelation zwischen drei herstellen soll
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
char *p [] = {"Straight Flush", "Four of a kind", "Full House", "Flush", "Straight", "Three of a kind", "Two Pair", "One Pair", "Skip Straight", "Round the Corner Straight", "Blaze", "Four Flush"};
int main (void) {
time_t t;
int i;
srand ((unsigned )time (\&t));
printf ("Vergleiche:n");
for (i = 0; i < 10; i++) {
printf ("%i) %stRt%sn", i, p [rand () % 12], p [rand () % 12]);
}
printf ("nBringe in die richtige Reihenfolge:n");
for (; i < 20; i++) {
printf ("%i) %s,t%s,t%sn", i, p [rand () % 12], p [rand () % 12],p [rand () % 12]);
}
return 0;
}
Vergleiche: 0) Straight R Four Flush 1) Skip Straight R Two Pair 2) Blaze R Skip Straight 3) Blaze R Skip Straight 4) Three of a kind R One Pair 5) Flush R One Pair 6) Full House R Flush 7) Full House R Two Pair 8) Four of a kind R Three of a kind 9) Flush R Blaze Bringe in die richtige Reihenfolge: 10) Two Pair, Straight, Three of a kind 11) Round the Corner Straight, Four Flush, Straight Flush 12) Straight, Three of a kind, Straight 13) Flush, Skip Straight, Skip Straight 14) Straight, Two Pair, Three of a kind 15) Straight, Straight, Three of a kind 16) Round the Corner Straight, Flush, Flush 17) Straight Flush, One Pair, Full House 18) Two Pair, Three of a kind, Skip Straight 19) Three of a kind, Two Pair, Two Pair

Ok, jetzt mache ich kurz eine Kaffee Pause, danach mache die weiteren Schriftlichen Rechenaufgaben, danach gehe ich in den Wald. wenn ich wieder da bin, mache ich Eulertour und Matrizenmultiplikation



Ich mache jetzt eine python 3 Aufgabe, dann Pause spaeter mache ich noch die Matrizenmultiplikation und spiele Klavier ohne Aufnahme
print (6+6)
print (5*7)
print (4-8)
x = 1 + 4
y = 2 + 5
z = 3 + 6
if x < y:
print ("Fall 1")
if y < z:
print ("Fall 1 von Fall 1")
else:
print ("Fall 2 von Fall 1")
else:
print ("Fall2")
if x < z:
print ("Fall 1 von Fall 2")
else:
print ("Fall 2 von Fall 2")
i = 0
while i < 10:
print (i+1)
i = i + 1
a = [1,4]
i = 3
while i <= 10:
a.append (i**2)
i = i + 1
i = 0
while i < 10:
print (a [i])
i = i + 1
b = a
b.reverse ()
print (b)
x = a.pop ()
print (x)
x = a.pop ()
print (x)
a = x * a
print (a)
a = a + b
print (a)
a.sort ()
print (a)
import math
print (math.sin (0.12321 * math.pi))
david@laptop-peaq:~\$ python3 python20240807.py 12 35 -4 Fall 1 Fall 1 von Fall 1 1 2 3 4 5 6 7 8 9 10 1 4 9 16 25 36 49 64 81 100 [100, 81, 64, 49, 36, 25, 16, 9, 4, 1] 1 4 [100, 81, 64, 49, 36, 25, 16, 9, 100, 81, 64, 49, 36, 25, 16, 9, 100, 81, 64, 49, 36, 25, 16, 9, 100, 81, 64, 49, 36, 25, 16, 9] [100, 81, 64, 49, 36, 25, 16, 9, 100, 81, 64, 49, 36, 25, 16, 9, 100, 81, 64, 49, 36, 25, 16, 9, 100, 81, 64, 49, 36, 25, 16, 9, 100, 81, 64, 49, 36, 25, 16, 9] [9, 9, 9, 9, 9, 16, 16, 16, 16, 16, 25, 25, 25, 25, 25, 36, 36, 36, 36, 36, 49, 49, 49, 49, 49, 64, 64, 64, 64, 64, 81, 81, 81, 81, 81, 100, 100, 100, 100, 100] 0.377482017783888
Ich mache jetzt einen Kaffee, dann die Matrizenmultiplikation





Da diese Matrix sehr gross ist lasse ich es fuer heute dabei
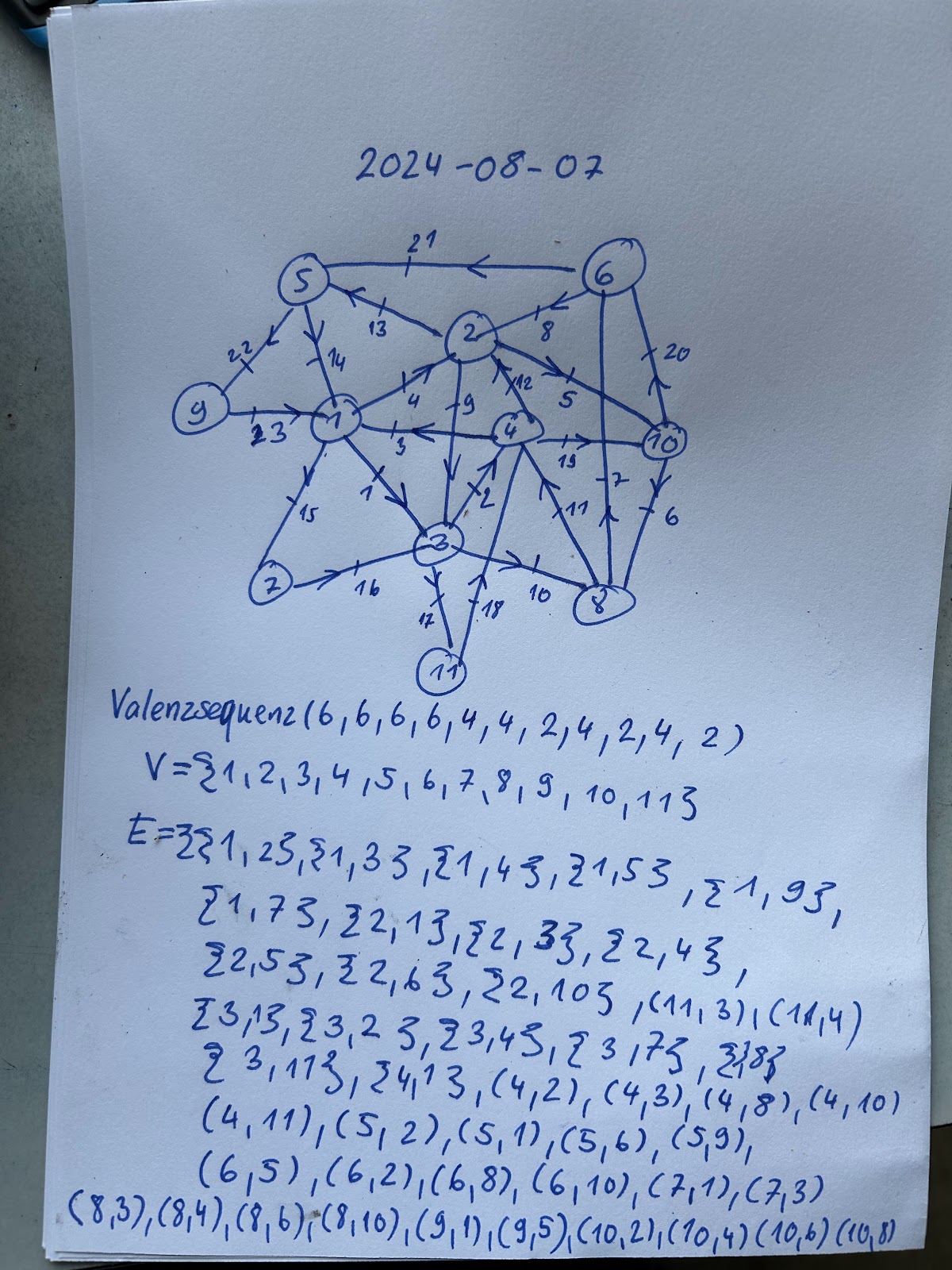
Zum Schluss vom Tage noch eine Figur := Gottheit zeichnen ueben
Ich entscheide mich fuer das